電子の比電荷

電気素量 $3$\displaystyle{e}$ $3$\displaystyle{ \[\text{C}\] }$ と電子の質量 $3$\displaystyle{m}$ $3$\displaystyle{ \[\text{kg}\] }$ の比 $3$\displaystyle{e/m}$ $3$\displaystyle{ \[\text{C/kg}\] }$ を電子の比電荷といい，その値は

$3$\displaystyle{ \frac{\hspace{2}e\hspace{2}}{\hspace{2}m\hspace{2}}=1.758820\times { 10 }^{ 11 }\text{\hspace{1}}\text{C/kg} }$

である．

＜電子の比電荷の測定（J. J. トムソンの実験）＞

希薄な気体の入ったガラス管内の陰極線に電場や磁場を加える実験において，陰極から飛び出した質量 $3$\displaystyle{m}$ $3$\displaystyle{ \[\text{kg}\] }$ ，電気量 $3$\displaystyle{- e}$ $3$\displaystyle{ \[\text{C}\] }$ の電子が，これらの電場や磁場に垂直に速さ $3$\displaystyle{\hspace{1}{v}_{0}}$ $3$\displaystyle{\[\text{m/s}\]}$ で入射する場合を考える．

● 電場への入射

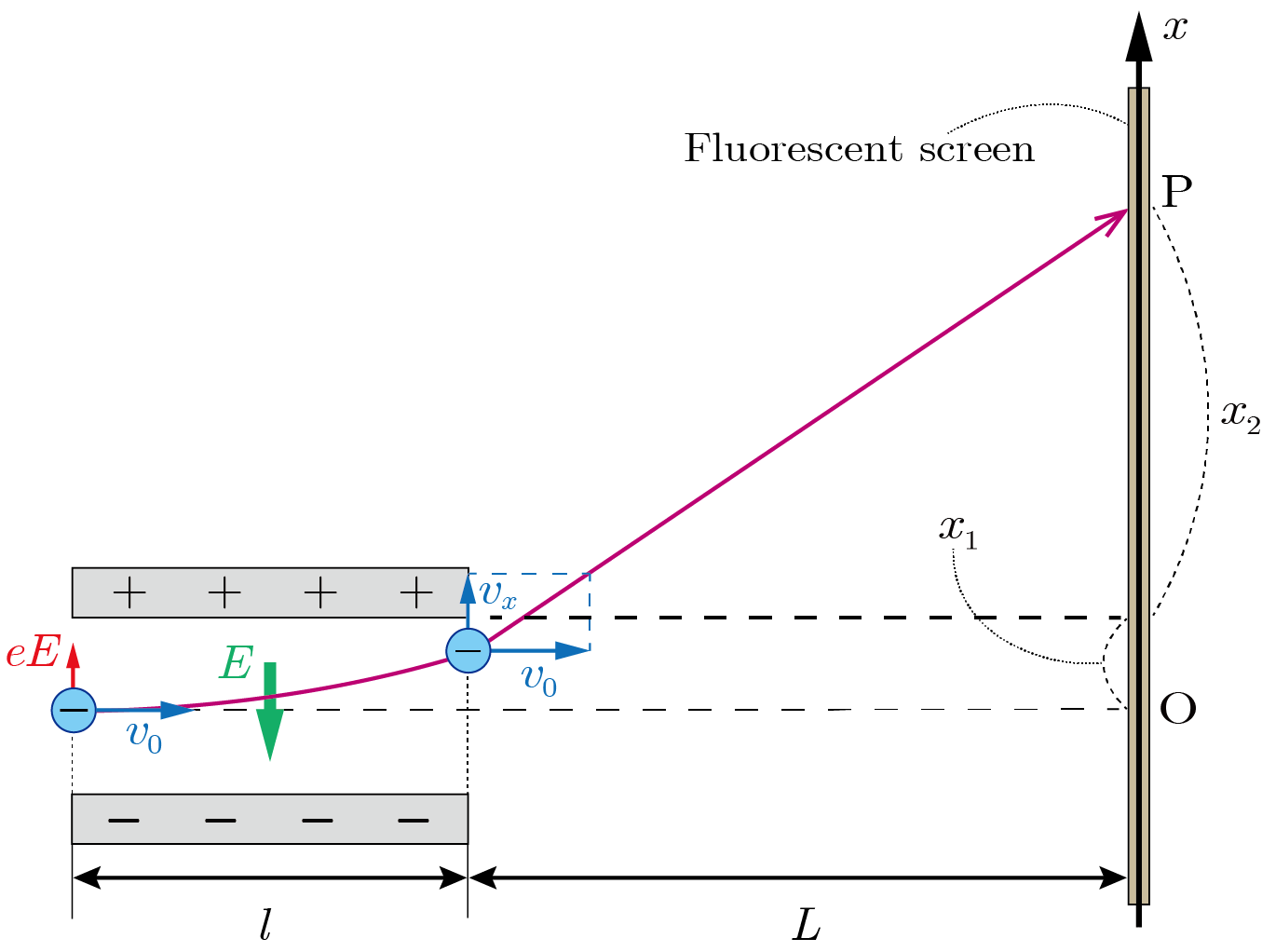
図1

図1のように電極間の一様な電場（強さ $3$\displaystyle{E}$ $3$\displaystyle{ \[\text{N/C}\] }$ ）に入射した電子は，電場が加わっている長さ $3$\displaystyle{l}$ $3$\displaystyle{ \[\text{m}\] }$ の区間において，電場と逆向き（ $3$\displaystyle{x}$ 軸の正の向き）に一定の大きさ $3$\displaystyle{F=eE}$ $3$\displaystyle{\[\text{N}\]}$ の静電気力を受け，放物運動（等加速度運動）を行う．電子は電場を抜け出た後，電極の端から $3$\displaystyle{L}$ $3$\displaystyle{ \[\text{m}\] }$ の位置に入射方向と垂直に置かれた蛍光板の点 $3$\displaystyle{\text{P}}$ に衝突し，輝点を生じる．

電子が電場を通過する時間 $3$\displaystyle{\hspace{1}{t}_{1}=l/\hspace{1}{v}_{0}}$ $3$\displaystyle{\[\text{s}\]}$ ，および加速度の $3$\displaystyle{x}$ 成分 $3$\displaystyle{\hspace{1}{a}_{x}= eE /m}$ $3$\displaystyle{\[ { \text{m/s} }^{\text{2}} \]}$ より，電子が電場を抜け出た瞬間の速度の $3$\displaystyle{x}$ 成分 $3$\displaystyle{\hspace{1}{v}_{x}}$ $3$\displaystyle{\[\text{m/s}\]}$ は

$3$\displaystyle{ \hspace{1}{v}_{x}=\hspace{1}{a}_{x}\hspace{1}{t}_{1} }$ $3$\displaystyle{ =\frac{\hspace{2} eE \hspace{2}}{\hspace{2}m\hspace{2}}\cdot \frac{\hspace{2}l\hspace{2}}{\hspace{2} \hspace{1}{v}_{0} \hspace{2}} }$ $3$\displaystyle{ =\frac{\hspace{2} eEl \hspace{2}}{\hspace{2} m\hspace{1}{v}_{0} \hspace{2}} }$

であり， $3$\displaystyle{x}$ の変位 $3$\displaystyle{\hspace{1}{x}_{1}}$ $3$\displaystyle{\[\text{m}\]}$ は

$3$\displaystyle{ \hspace{1}{x}_{1}=\frac{\hspace{2}1\hspace{2}}{\hspace{2}2\hspace{2}}\hspace{1}{a}_{x}t_{1}^{2} }$ $3$\displaystyle{ =\frac{\hspace{2}1\hspace{2}}{\hspace{2}2\hspace{2}}\cdot \frac{\hspace{2} eE \hspace{2}}{\hspace{2}m\hspace{2}}\cdot { $ \frac{\hspace{2}l\hspace{2}}{\hspace{2} \hspace{1}{v}_{0} \hspace{2}} $ }^{2} }$ $3$\displaystyle{ =\frac{\hspace{2} eE{l}^{2} \hspace{2}}{\hspace{2} 2mv_{0}^{2} \hspace{2}} }$

である．電場を出てから点 $3$\displaystyle{\text{P}}$ に達するまでの時間は $3$\displaystyle{\hspace{1}{t}_{2}=L/\hspace{1}{v}_{0}}$ $3$\displaystyle{\[\text{s}\]}$ であり，その間，電子は等速直線運動をするため， $3$\displaystyle{x}$ 方向の変位 $3$\displaystyle{\hspace{1}{x}_{2}}$ $3$\displaystyle{\[\text{m}\]}$ は

$3$\displaystyle{ \hspace{1}{x}_{2}=\hspace{1}{v}_{x}\hspace{1}{t}_{2} }$ $3$\displaystyle{ =\frac{\hspace{2} eEl \hspace{2}}{\hspace{2} m\hspace{1}{v}_{0} \hspace{2}}\cdot \frac{\hspace{2}L\hspace{2}}{\hspace{2} \hspace{1}{v}_{0} \hspace{2}}=\frac{\hspace{2} eElL \hspace{2}}{\hspace{2} mv_{0}^{2} \hspace{2}} }$

である．よって， $3$\displaystyle{\text{P}}$ の位置は

$3$\displaystyle{ x=\hspace{1}{x}_{1}+\hspace{1}{x}_{2} }$ $3$\displaystyle{ =\frac{\hspace{2} eE{l}^{2} \hspace{2}}{\hspace{2} 2mv_{0}^{2} \hspace{2}}+\frac{\hspace{2} eElL \hspace{2}}{\hspace{2} mv_{0}^{2} \hspace{2}}=\frac{\hspace{2} eEl \hspace{2}}{\hspace{2} mv_{0}^{2} \hspace{2}} $ L+\frac{\hspace{2}l\hspace{2}}{\hspace{2}2\hspace{2}} $ }$ $3$\displaystyle{ \text{\hspace{5}}\cdots $1$ }$

となる．

● 磁場への入射

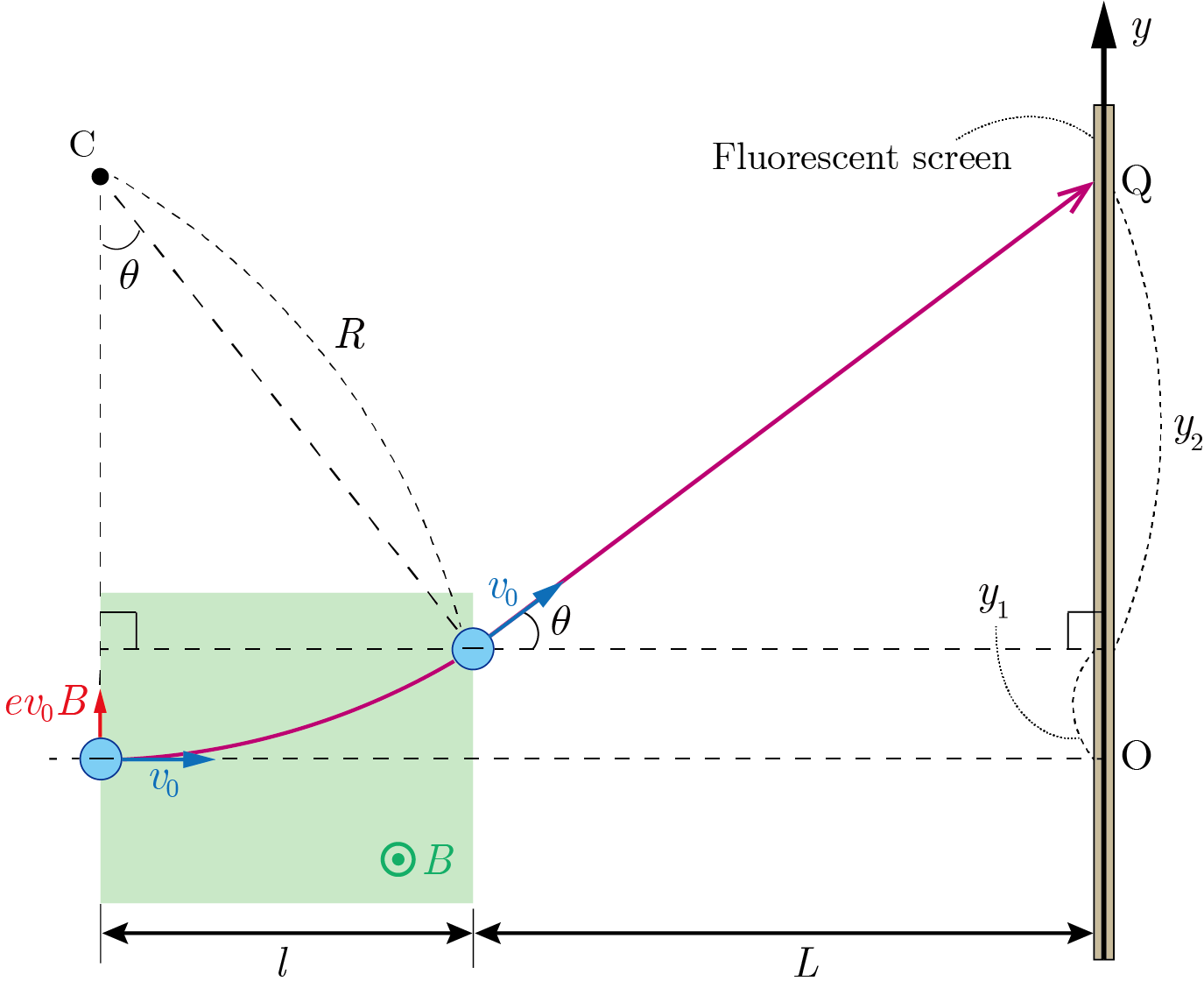
図2

図2のように，一様な磁場（図面奥から手前の向きに，強さ $3$\displaystyle{B}$ $3$\displaystyle{\[\text{T}\]}$ の磁束密度）に垂直に入射した電子は，磁場が加わっている長さ $3$\displaystyle{l}$ $3$\displaystyle{\[\text{m}\]}$ の領域（淡緑部）において，磁場から大きさ $3$\displaystyle{F=e\hspace{1}{v}_{0}B}$ $3$\displaystyle{\[\text{N}\]}$ のローレンツ力を受けて半径 $3$\displaystyle{R}$ $3$\displaystyle{\[\text{m}\]}$ の等速円運動を行う．ローレンツ力が向心力となっているので，電子の運動方程式（の動径方向成分）は

$3$\displaystyle{ m\frac{\hspace{2} v_{0}^{2} \hspace{2}}{\hspace{2}R\hspace{2}}=e\hspace{1}{v}_{0}B }$

であり，半径は

$3$\displaystyle{ R=\frac{\hspace{2} m\hspace{1}{v}_{0} \hspace{2}}{\hspace{2} eB \hspace{2}} }$

と表される．電子が磁場を抜け出た瞬間の $3$\displaystyle{y}$ 方向の変位を $3$\displaystyle{\hspace{1}{y}_{1}}$ $3$\displaystyle{\[\text{m}\]}$ とすると，三平方の定理より

$3$\displaystyle{ {R}^{2}- { $ R- \hspace{1}{y}_{1} $ }^{2}={l}^{2} }$ $3$\displaystyle{ \text{\hspace{5}}\Rightarrow \text{\hspace{5}}\hspace{1}{y}_{1} $ 2R- \hspace{1}{y}_{1} $ ={l}^{2} }$

であり，軌道の曲げられ方が十分小さい（ $3$\displaystyle{R}$ に比べて $3$\displaystyle{\hspace{1}{y}_{1}}$ が十分に小さい）場合には

$3$\displaystyle{ \hspace{1}{y}_{1}=\frac{\hspace{2} {l}^{2} \hspace{2}}{\hspace{2} 2R- \hspace{1}{y}_{1} \hspace{2}} }$ $3$\displaystyle{ \approx \frac{\hspace{2} {l}^{2} \hspace{2}}{\hspace{2} 2R \hspace{2}}=\frac{\hspace{2} eB{l}^{2} \hspace{2}}{\hspace{2} 2m\hspace{1}{v}_{0} \hspace{2}} }$

と表せる．磁場を出てから蛍光板の点 $3$\displaystyle{\text{Q}}$ に達するまでの間，電子は等速直線運動をするので， $3$\displaystyle{y}$ 方向の変位 $3$\displaystyle{\hspace{1}{y}_{2}}$ $3$\displaystyle{\[\text{m}\]}$ は

$3$\displaystyle{ \hspace{1}{y}_{2}=L\tan {\theta}=L\frac{\hspace{2}l\hspace{2}}{\hspace{2} R- \hspace{1}{x}_{1} \hspace{2}}\approx \frac{\hspace{2} lL \hspace{2}}{\hspace{2}R\hspace{2}} }$ $3$\displaystyle{ =\frac{\hspace{2} eBlL \hspace{2}}{\hspace{2} m\hspace{1}{v}_{0} \hspace{2}} }$

となる．よって点 $3$\displaystyle{\text{Q}}$ の位置は

$3$\displaystyle{ y=\hspace{1}{y}_{1}+\hspace{1}{y}_{2} }$ $3$\displaystyle{ =\frac{\hspace{2} eB{l}^{2} \hspace{2}}{\hspace{2} 2m\hspace{1}{v}_{0} \hspace{2}}+\frac{\hspace{2} eBlL \hspace{2}}{\hspace{2} m\hspace{1}{v}_{0} \hspace{2}} }$ $3$\displaystyle{ =\frac{\hspace{2} eBl \hspace{2}}{\hspace{2} m\hspace{1}{v}_{0} \hspace{2}} $ L+\frac{\hspace{2}l\hspace{2}}{\hspace{2}2\hspace{2}} $ }$ $3$\displaystyle{ \text{\hspace{5}}\cdots $2$ }$

となる． $3$\displaystyle{\hspace{1}{v}_{0}}$ , $3$\displaystyle{l}$ , $3$\displaystyle{L}$ は式 $3$\displaystyle{ $1$ }$ , $3$\displaystyle{ $2$ }$ で同じ値を取るものとして，この2式から $3$\displaystyle{\hspace{1}{v}_{0}}$ を消去すると

$3$\displaystyle{ \frac{\hspace{2} {y}^{2} \hspace{2}}{\hspace{2}x\hspace{2}}=\frac{\hspace{2} e{B}^{2}l \hspace{2}}{\hspace{2} mE \hspace{2}} $ L+\frac{\hspace{2}l\hspace{2}}{\hspace{2}2\hspace{2}} $ }$ $3$\displaystyle{ \text{\hspace{5}}\Rightarrow \text{\hspace{5}} }$ $3$\displaystyle{ \frac{\hspace{2}e\hspace{2}}{\hspace{2}m\hspace{2}}=\frac{\hspace{2} 2E \hspace{2}}{\hspace{2} {B}^{2}l $ 2L+l $ \hspace{2}}\cdot \frac{\hspace{2} {y}^{2} \hspace{2}}{\hspace{2}x\hspace{2}} }$ $3$\displaystyle{ \text{\hspace{5}}\cdots $3$ }$

が求まる．

したがって，電子と電場に入射する速さと磁場に入射する速さを同じ値（ $3$\displaystyle{\hspace{1}{v}_{0}}$ ）に設定し，蛍光板に衝突した位置 $3$\displaystyle{x}$ ， $3$\displaystyle{y}$ を測定することによって，式 $3$\displaystyle{ $3$ }$ から電子の比電荷を見積もることができる．比電荷は陰極の金属や管内の気体の種類によらず常に一定の値 $3$\displaystyle{e/m=1.758820\times {10}^{11}}$ $3$\displaystyle{\text{C/kg}}$ をとり，金属には共通の電子が含まれていることが分かる．

ホーム>>物理>>第5編原子>>第1章電子と光>>電子の比電荷

学生スタッフ作成

最終更新日： 2025年11月12日