三角関数の合成問題

■問題

次の関数を $3$\displaystyle{ r\sin ${\theta}+{\alpha}$ }$ の形に表せ．ただし， $3$\displaystyle{ r> 0 }$ ， $3$\displaystyle{ - {\pi}< {\theta}< {\pi} }$ とする．

$3$\displaystyle{ \sqrt{6}\sin {\theta}+\sqrt{2}\cos {\theta} }$

■解説動画

◆三角関数の動画一覧のページへ

■答

$3$\displaystyle{2\sqrt{2}\sin \left({ {\theta}+\frac{\hspace{2}{\pi}\hspace{2}}{\hspace{2}6\hspace{2}} }\right)}$

■ヒント

三角関数の合成公式

$3$\displaystyle{ a\sin {\theta}+b\cos {\theta} }$ $3$\displaystyle{ =\sqrt{ {a}^{2}+{b}^{2} }\sin \left({ {\theta}+\alpha }\right) }$

を利用する．

■解答

$3$\displaystyle{r=\sqrt{ {a}^{2}+{b}^{2} }}$ $3$\displaystyle{=\sqrt{ { \sqrt{6} }^{2}+{ \sqrt{2} }^{2} }}$ $3$\displaystyle{=2\sqrt{2}}$

より

$3$\displaystyle{ \sqrt{6}\sin {\theta}+\sqrt{2}\cos {\theta} }$ $3$\displaystyle{=2\sqrt{2}\left({ \frac{\hspace{2} \sqrt{6} \hspace{2}}{\hspace{2} 2\sqrt{2} \hspace{2}}\sin {\theta}+\frac{\hspace{2} \sqrt{2} \hspace{2}}{\hspace{2} 2\sqrt{2} \hspace{2}}\cos {\theta} }\right)}$ $3$\displaystyle{=2\sqrt{2}\left({ \frac{\hspace{2} \sqrt{3} \hspace{2}}{\hspace{2}2\hspace{2}}\sin {\theta}+\frac{\hspace{2}1\hspace{2}}{\hspace{2}2\hspace{2}}\cos {\theta} }\right)}$ ･･････(1)

と式を変形する．

三角関数の合成公式より

$3$\displaystyle{ \sqrt{6}\sin {\theta}+\sqrt{2}\cos {\theta} }$ $3$\displaystyle{=2\sqrt{2}\sin \left({ {\theta}+\alpha }\right)}$ ･･････(2)

の形に変形できる．(2)に加法定理を適用すると

$3$\displaystyle{=2\sqrt{2}\sin \left({ {\theta}+\alpha }\right)}$ $3$\displaystyle{=2\sqrt{2}\left({ \sin {\theta}\cos \alpha +\cos {\theta}\sin \alpha }\right)}$ ･･････(3)

となる．

(1)と(3)を比較すると

$3$\displaystyle{\left{{ \begin{array}{lll} \cos \alpha =\displaystyle{\frac{\hspace{2} \sqrt{3} \hspace{2}}{\hspace{2}2\hspace{2}}} & \vspace{6}\\ \sin \alpha =\displaystyle{\frac{\hspace{2}1\hspace{2}}{\hspace{2}2\hspace{2}}} & \vspace{6}\\ \end{array} }$

となる連立方程式が得られる．これを解く．

$3$\displaystyle{ \cos \alpha =\frac{\hspace{2} \sqrt{3} \hspace{2}}{\hspace{2}2\hspace{2}} }$ より， $3$\displaystyle{\alpha =- \frac{\hspace{2}{\pi}\hspace{2}}{\hspace{2}6\hspace{2}},\frac{\hspace{2}{\pi}\hspace{2}}{\hspace{2}6\hspace{2}}}$ 　･･････(4)　(計算はここを参照)

$3$\displaystyle{ \sin \alpha =\frac{\hspace{2}1\hspace{2}}{\hspace{2}2\hspace{2}} }$ より， $3$\displaystyle{\alpha =\frac{\hspace{2}{\pi}\hspace{2}}{\hspace{2}6\hspace{2}},\frac{\hspace{2}5\hspace{2}}{\hspace{2}6\hspace{2}}{\pi}}$ 　･･････(5)　(計算はここを参照)

(4)，(5)より

$3$\displaystyle{ {\alpha}=\frac{\hspace{2}{\pi}\hspace{2}}{\hspace{2}6\hspace{2}} }$

となる．したがって

$3$\displaystyle{ \sqrt{6}\sin {\theta}+\sqrt{2}\cos {\theta} }$ $3$\displaystyle{=2\sqrt{2}\left({ \cos \frac{\hspace{2}{\pi}\hspace{2}}{\hspace{2}6\hspace{2}}\sin {\theta}+\sin \frac{\hspace{2}{\pi}\hspace{2}}{\hspace{2}6\hspace{2}}\cos {\theta} }\right)}$ $3$\displaystyle{=2\sqrt{2}\sin \left({ {\theta}+\frac{\hspace{2}{\pi}\hspace{2}}{\hspace{2}6\hspace{2}} }\right)}$

となる．

●作図より求める方法

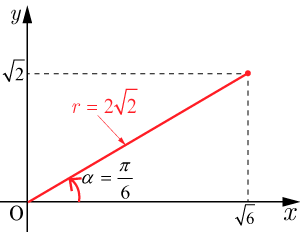
座標平面上に， $3$\displaystyle{ \sin }$ の係数 $3$\displaystyle{ 1 }$ を $3$\displaystyle{ x }$ 成分， $3$\displaystyle{ \cos }$ の係数 $3$\displaystyle{ -1 }$ を $3$\displaystyle{ y }$ 成分とする点 $3$\displaystyle{\text{P}}$ と原点 $3$\displaystyle{\text{O}}$ を結ぶ線分 $3$\displaystyle{\text{OP}}$ を描く．線分 $3$\displaystyle{\text{OP}}$ の長さが $3$\displaystyle{r}$ ，線分 $3$\displaystyle{\text{OP}}$ と $3$\displaystyle{ x }$ 軸となす角が角度 $3$\displaystyle{ {\alpha} }$ となる．

よって

$3$\displaystyle{r=2\sqrt{2}}$ ， $3$\displaystyle{ {\alpha}=\frac{\hspace{2}{\pi}\hspace{2}}{\hspace{2}6\hspace{2}} }$

$3$\displaystyle{ \sqrt{6}\sin {\theta}+\sqrt{2}\cos {\theta} }$ $3$\displaystyle{=2\sqrt{2}\sin \left({ {\theta}+\frac{\hspace{2}{\pi}\hspace{2}}{\hspace{2}6\hspace{2}} }\right)}$

となる．

■グラフ

ホーム>>カテゴリー分類>>三角関数>>三角関数の問題>>三角関数の合成>>三角関数の合成問題（ $3$\displaystyle{ \sqrt{6}\sin {\theta}+\sqrt{2}\cos {\theta} }$ ）

学生スタッフ作成

最終更新日： 2025年3月12日