| ||||||||||||
|
平面図形の重心を求める問題
■問題
直線
と曲線
で囲まれた図形の重心
の位置を求めよ.ただし,重心
の
座標を
,
座標を
とする.
■答
■ヒント
平面の重心の計算より
の公式を用いる.
■解説
●図形の面積 を求める
を求める
まず,直線
と曲線
の交点を求める.
・・・・・・(1) ・・・・・・(2) |
(1)を(2)に代入する.
・・・・・・(3)
(3)を
について解く.
,
,
・・・・・・(4)
(4)と(1)より,交点座標は
,
となる.
よって,求める面積は(面積の求め方は,面積の計算を参照)
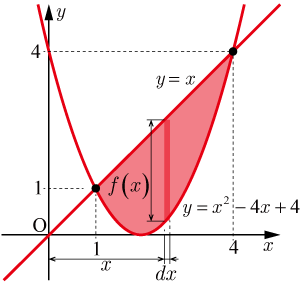
● を求める
を求める
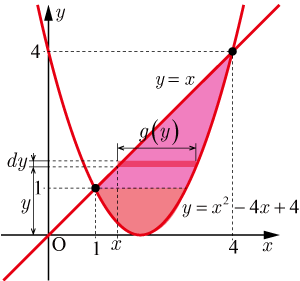
● を求める
を求める
まず,
を求める.
の範囲によって
が異なることに注意する.
より
となる.
のとき
のとき
よって
・・・・・・(5)
となる.積分は個別に計算することにする.
・・・・・・(6)
・・・・・・(7)
(6),(7)を(5)に代入する
よって,図形の重心
の位置は
となる.
ホーム>>カテゴリー分類>>積分>>積分の問題>>定積分の問題
>>
,
で囲まれた図形の重心
学生スタッフ作成
最終更新日:
2023年11月24日