2次関数のグラフ　 $y = x^{2}$

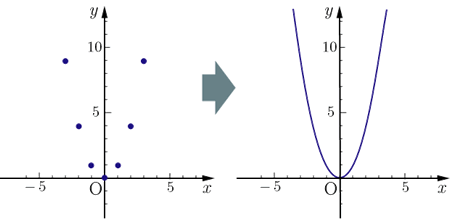
2次関数の最も簡単な関数は $y = x^{2}$ である．この関数についてグラフを考える．

$x$ の値-3，-2，-1，0，1，2，3に対する $y$ の値をを下の表に示す．

$x$ の値	-3	-2	-1	0	1	2	3
$y$ の値	9	4	1	0	1	4	9

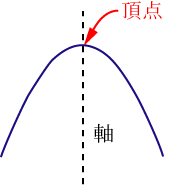
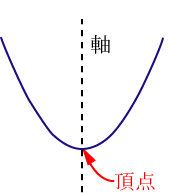
各 $x$ ， $y$ の組に対応する点を座標平面に描くと左下の図のようになる．表のような $y = x^{2}$ の関係を満たす点を集めてグラフにすると右下の図のようのような曲線になる．このような2次関数のグラフを放物線ともいう．

放物線の対称軸を，その放物線の軸といい，軸と放物線との交点を，その放物線の頂点という．

$y = x^{2}$ の場合，軸は $y$ 軸で，頂点は原点になる(上の図を参照)．

頂点についての説明図は，下の図を参照すること．

ホーム>>カテゴリー分類>>関数>>2次関数のグラフ $y = x^{2}$

最終更新日： 2022年5月25日

2次関数のグラフ y= x 2