平面の方程式 

点 $\text{P}$ $\left(x_0,y_0,z_0\right)$ を通り，法線ベクトルが $\overrightarrow{n}=\left(a,b,c\right)$ の平面の方程式は

$a\left(x-x_0\right)+b\left(y-y_0\right)+c\left(z-z_0\right)=0$

と表わされる．また，平面の方程式は一般に

$ax+by+cz+d=0$   （一般形）

と表される．このとき，平面の法線ベクトルは ${\displaystyle \overrightarrow{n}=\left(a,b,c\right)}$ となる．

■平面の方程式の導出

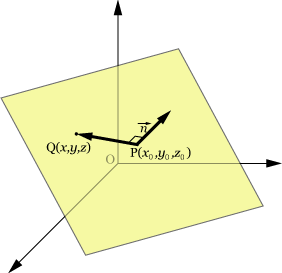平面は，空間中の点と平面に垂直な法線ベクトルが決まれば，一意的に決まる．平面上の点 $\text{P}$ の座標を ${\displaystyle \left(x_0,y_0,z_0\right)}$ ，法線ベクトルを ${\displaystyle \overrightarrow{n}=\left(a,b,c\right)}$ とし，平面上の任意の点 $\text{Q}$ の座標を ${\displaystyle \left(x,y,z\right)}$ とすると，ベクトル ${\displaystyle \stackrel{⟶}{\text{PQ}}}$ は平面に含まれる． ${\displaystyle \overrightarrow{n}}$ は平面の法線ベクトルなので， ${\displaystyle \overrightarrow{n}}$ と ${\displaystyle \stackrel{⟶}{\text{PQ}}}$ のなす角は90°である．よって内積がゼロとなるので

${\displaystyle \overrightarrow{n}·\stackrel{⟶}{\text{PQ}}=0}$    

となる．この関係から

${\displaystyle \begin{array}{l}\left(a,b,c\right)·\left(x-x_0,y-y_0,z-z_0\right)=0\\ a\left(x-x_0\right)+b\left(y-y_0\right)+c\left(z-z_0\right)=0\end{array}}$

となり，平面の方程式が求まる．

■平面の方程式の求め方のいろいろ】

●空間中の3点で決まる平面の方程式

空間中の3点を $\text{A}$ ${\displaystyle \left(a_x,a_y,a_z\right)}$ ， $\text{B}$ ${\displaystyle \left(b_x,b_y,b_z\right)}$ ， $\text{C}$ ${\displaystyle \left(c_x,c_y,c_z\right)}$ を含む平面の方程式の求め方．

●方法1

3点を含む平面上の点をP ${\displaystyle \left(x,y,z\right)}$ とすると， ${\displaystyle \stackrel{⟶}{\text{AB}}}$ と ${\displaystyle \stackrel{⟶}{\text{AC}}}$ を用いて ${\displaystyle \stackrel{⟶}{\text{AP}}}$ を表すと

${\displaystyle m\stackrel{⟶}{\text{AB}}+n\stackrel{⟶}{\text{AC}}=\stackrel{⟶}{\text{AP}}}$

となる． m ， n は媒介変数．これを座標で表すと

となり，整理すると

${\displaystyle (m\left(b_x-a_x\right)+n\left(c_x-a_x\right),}$ ${\displaystyle m\left(b_y-a_y\right)+n\left(c_y-a_y\right),}$ ${\displaystyle m\left(b_z-a_z\right)+n\left(c_z-a_z\right))}$ ${\displaystyle =\left(x-a_x,y-a_y,z-a_z\right)}$

となる．各座標を比べると

となる．この関係式から， m ， n を消去すると平面の方程式が得られる．

●方法2

平面の方程式の一般形の ${\displaystyle ax+by+cz+d=0}$ に点 $\text{A}$ ，点 $\text{B}$ ，点 $\text{C}$ の座標を代入して得られる連立方程式

${\displaystyle \{\begin{array}{l}a·a_x+b·a_y+c·a_z+d=0\\ a·b_x+b·b_y+c·b_z+d=0\\ a·c_x+b·c_y+c·c_z+d=0\end{array}}$

を解いても3点を含む平面の方程式を求めることができる．

●方法3

平面の法線ベクトル ${\displaystyle \overrightarrow{n}}$ を

${\displaystyle \overrightarrow{n}=\left(l,m,n\right)}$

とする．

${\displaystyle \overrightarrow{\text{A}\text{B}}\cdot \overrightarrow{n}=0}$

${\displaystyle \overrightarrow{\text{A}\text{C}}\cdot \overrightarrow{n}=0}$  

より， ${\displaystyle \overrightarrow{n}=\left(l,m,n\right)}$ を求める．

点 ${\displaystyle \text{A}\left(a_x,a_y,a_z\right)}$ を通り，法線ベクトルが ${\displaystyle \overrightarrow{n}=\left(l,m,n\right)}$ より，平面の方程式は

${\displaystyle l\left(x-a_x\right)+m\left(y-a_y\right)+n\left(z-a_z\right)=0}$

となる．

●方法4

平面の法線ベクトル ${\displaystyle \overrightarrow{n}}$ は外積を用いると

${\displaystyle \overrightarrow{n}=\overrightarrow{\text{A}\text{B}}\times \overrightarrow{\text{A}\text{C}}}$

となる．

法線ベクトル ${\displaystyle \overrightarrow{n}}$ が求まり，平面は点 ${\displaystyle \text{A}}$ を通ることより，平面の方程式を求めることができる．

 

ホーム>>カテゴリー分類>>関数>>平面の方程式

最終更新日： 2025年4月22日