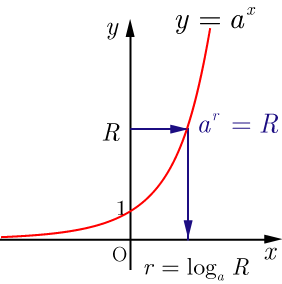
対数の定義

$a>0$ ， ${\displaystyle a\ne 1}$ とするとき，どのような正の数 R に対しても

${\displaystyle a^r=R}$

を満たす実数 r が，ただ1つ定まる（参照）．この r の値を， a を底とする R の対数といい

${\displaystyle r={log}_{a}R}$

で表す． R をこの対数の真数といい，

${\displaystyle R>0}$

である． ${\displaystyle R>0}$ のことを真数条件という．

対数の定義より，指数と対数の間には

${\displaystyle r={log}_{a}R\iff a^r=R}$

となる関係が成り立つ．

■関連動画

■対数の性質

$a>0$ ， $a\ne 1$ ， $R>0$ ， $S>0$ とするとき

• ${log}_{a}RS={log}_{a}R+{log}_{a}S$   ⇒証明

• ${\displaystyle {log}_a\frac{R}{S}={log}_{a}R-{log}_{a}S}$   ⇒証明

• ${log}_a{R}^t=t{log}_{a}R$   ⇒証明

• ${log}_{a}a=1$    ${\displaystyle \left(\because a^1=a\right)}$    ⇒ 証明

• ${log}_{a}1=0$    ${\displaystyle \left(\because a^0=1\right)}$    ⇒ 証明

• ${\displaystyle {log}_{a}R=\frac{{log}_{b}R}{{log}_{b}a}}$   ⇒証明

 

ホーム>>カテゴリー別分類>>指数/対数>>対数の定義

最終更新日： 2025年4月26日