三角形の面積

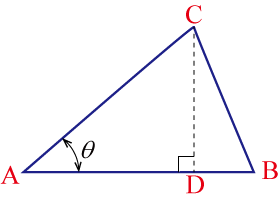${\displaystyle \Delta \text{ABC}}$ の面積を $S$ とする

${\displaystyle S=\frac{1}{2}\text{AB}·\text{AC}·sin\theta }$ 　･･････(1)

となる．

ベクトルを用いて表すと

${\displaystyle S=\frac{1}{2}\sqrt{{\left|\stackrel{⟶}{\text{AB}}\right|}^2·{\left|\stackrel{⟶}{\text{AC}}\right|}^2-{\left(\stackrel{⟶}{\text{AB}}·\stackrel{⟶}{\text{AC}}\right)}^2}}$ 　･･････(2)

となる．この式は，頂点 ${\displaystyle \text{A}}$ ， ${\displaystyle \text{B}}$ ， ${\displaystyle \text{C}}$ の座標が与えられているときに便利である．

$\Delta \text{ABC}$が座標平面上にあり，${\displaystyle \overrightarrow{\text{AB}}=\left(x_1,y_1\right)}$ ，${\displaystyle \overrightarrow{\text{AC}}=\left(x_2,y_2\right)}$ とすると

${\displaystyle S=\frac{1}{2}\left|x_1{y}_2-x_2{y}_1\right|}$　･･････(3)

となる．

●参考

• ヘロンの公式： ${\displaystyle S=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}$
• 外積を用いた場合： ${\displaystyle S=\frac{1}{2}\left|\overrightarrow{\text{AB}}\times \overrightarrow{\text{AB}}\right|}$

■導出方法

$\Delta \text{ABC}$ のへ底辺を $\text{AB}$ ，高さを $\text{CD}$ とすると， $\Delta \text{ABC}$ の面積 $S$ は

${\displaystyle S=\frac{1}{2}\text{AB}\cdot \text{CD}}$   ･･････（4）

である．また，三角比の定義より

${\displaystyle \text{CD}=\text{AC}\sin \theta }$   ･･････（5）

である．

(4)に(5)を代入すると

${\displaystyle S=\frac{1}{2}\text{AB}·\text{AC}·sin\theta }$

となり，(1)が得られる．

また

$\text{AB}=\left|\stackrel{⟶}{\text{AB}}\right|$ ， $\text{AC}=\left|\stackrel{⟶}{\text{AC}}\right|$   ･･････（6）

内積の定義より

${\displaystyle cos\theta =\frac{\stackrel{⟶}{\text{AB}}·\stackrel{⟶}{\text{AC}}}{\left|\stackrel{⟶}{\text{AB}}\right|·\left|\stackrel{⟶}{\text{AC}}\right|}}$ ･･････（7）

${\sin }^2\theta +{\cos }^2\theta =1$ より

$sin\theta =\sqrt{1-{cos}^2\theta }$  ･･････（8）

である．

(1)に(6)を代入すると

${\displaystyle S=\frac{1}{2}\left|\overrightarrow{\text{AB}}\right|\cdot \left|\overrightarrow{\text{AC}}\right|\sin \theta }$  ･･････（9）

(9)になり，さらに，(9)に(8)を代入すると

${\displaystyle S=\frac{1}{2}\left|\overrightarrow{\text{AB}}\right|\cdot \left|\overrightarrow{\text{AC}}\right|\sqrt{1-{\cos }^2\theta }}$  ･･････（10）

(10)になり，さらに，(10)に(7)を代入すると

となり(2)が得られる．

${\displaystyle \left|\overrightarrow{\text{AB}}\right|=\sqrt{x_1{}^2+y_1{}^2}}$　･･････(11)

${\displaystyle \left|\overrightarrow{\text{AC}}\right|=\sqrt{x_2{}^2+y_2{}^2}}$　･･････(12)

${\displaystyle \overrightarrow{\text{AB}}\cdot \overrightarrow{\text{AC}}=\left(x_1,y_1\right)\cdot \left(x_2,y_2\right)}$${\displaystyle =x_1{x}_2+y_1{y}_2}$　･･････(13)

(2)に(11)，(12)，(13)を代入する．

${\displaystyle S=\frac{1}{2}\sqrt{\left(x_1{}^2+y_1{}^2\right)\left(x_2{}^2+y_2{}^2\right)-{\left(x_1{x}_2+y_1{y}_2\right)}^2}}$

${\displaystyle =\frac{1}{2}\sqrt{x_1{}^2{x}_2{}^2+x_1{}^2{y}_2{}^2+x_2{}^2{y}_1{}^2+y_1{}^2{y}_2{}^2-x_1{}^2{x}_2{}^2-2x_1{x}_2{y}_1{y}_2-y_1{}^2{y}_2{}^2}}$

${\displaystyle =\frac{1}{2}\sqrt{x_1{}^2{y}_2{}^2+x_2{}^2{y}_1{}^2-2x_1{x}_2{y}_1{y}_2}}$

${\displaystyle =\frac{1}{2}\sqrt{{\left(x_1{y}_2-x_2{y}_1\right)}^2}}$

${\displaystyle =\frac{1}{2}\left|x_1{y}_2-x_2{y}_1\right|}$

となり，(3)が得られた．

 

ホーム>>カテゴリー分類>>ベクトル>>三角形の面積

最終更新日： 2025年10月31日