演習問題
■式の展開と因数分解に関する問題3x2+xy+15x−2y2−5y+12
■分数式の計算
■部分分数の分解
次の分数を部分分数に分解しなさい.
6x2+4x+3
次の分数を部分分数に分解しなさい.
2x+1x2+x−2
次の分数を部分分数に分解しなさい.
5x+1x2−x−12
次の分数を部分分数に分解しなさい.
6x−2x2−3x−10
次の分数を部分分数に分解しなさい.
2x+4x2+4x−12
次の問題を積分せよ(不定積分).
∫1√9−x2dx
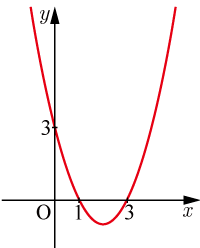
■2次関数のグラフの式を求める問題
■2次方程式に関する問題
■2次方程式に関する問題
■2次方程式に関する問題
■2次方程式に関する問題
■3次方程式に関する問題
■3次方程式に関する問題