概念問題 解答

線形代数　行列式

問題3の解答

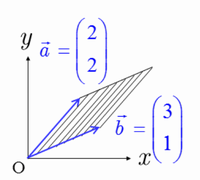
$z$軸も取り入れた座標空間として考えると， 斜線部の平行四辺形の面積は， $\overrightarrow{a}=\left(2,2,0\right)$ と$\overrightarrow{b}=\left(3,1,0\right)$ の外積の大きさ $\left|\overrightarrow{a}\times \overrightarrow{b}\right|$ と等しい．

行列式を用いて外積の計算をすると

$\overrightarrow{a}\times \overrightarrow{b}=\left|\begin{array}{ccc}\overrightarrow{i}& \overrightarrow{j}& \overrightarrow{k}\\ 2& 2& 0\\ 3& 1& 0\end{array}\right|$

$=\left|\begin{array}{cc}2& 0\\ 1& 0\end{array}\right|\overrightarrow{i}-\left|\begin{array}{cc}2& 0\\ 3& 0\end{array}\right|\overrightarrow{j}+\left|\begin{array}{cc}2& 2\\ 3& 1\end{array}\right|\overrightarrow{k}$

$=\left|\begin{array}{cc}2& 2\\ 3& 1\end{array}\right|\overrightarrow{k}$

$\overrightarrow{a}\times \overrightarrow{b}$の方向は$z$軸と逆方向であるので，行列式$\left|\begin{array}{cc}2& 2\\ 3& 1\end{array}\right|$の値は負の値である．よって，

$\left|\overrightarrow{a}\times \overrightarrow{b}\right|=-\left|\begin{array}{cc}2& 2\\ 3& 1\end{array}\right|$　･･････(1)

となる．(1)を以下のように変形する．

行列式の行または列の入れ替えの性質を利用して1行と2行を入れかえる.

$=\left|\begin{array}{cc}3& 1\\ 2& 2\end{array}\right|$

行列式の転置の性質を利用して，行と列を入れかえる．

$=\left|\begin{array}{cc}3& 2\\ 1& 2\end{array}\right|$

この行列式の値が斜線部の平行四辺形の面積となる．

また，2次の行列式の幾何学的な意味を参考にすると，斜線部の平行四辺形の面積は

$\left|\begin{array}{cc}3& 2\\ 1& 2\end{array}\right|$

となる．

よって，3が正解となる．