等加速度運動 (uniformly accelerated motion)
物体の加速度が一定で変化しない(加速度の大きさも向きも変化しない)運動を等加速度運動 (uniformly accelerated motion)という.運動方程式から,物体の加速度が一定ということは,その物体に作用する合力が一定であるということである.
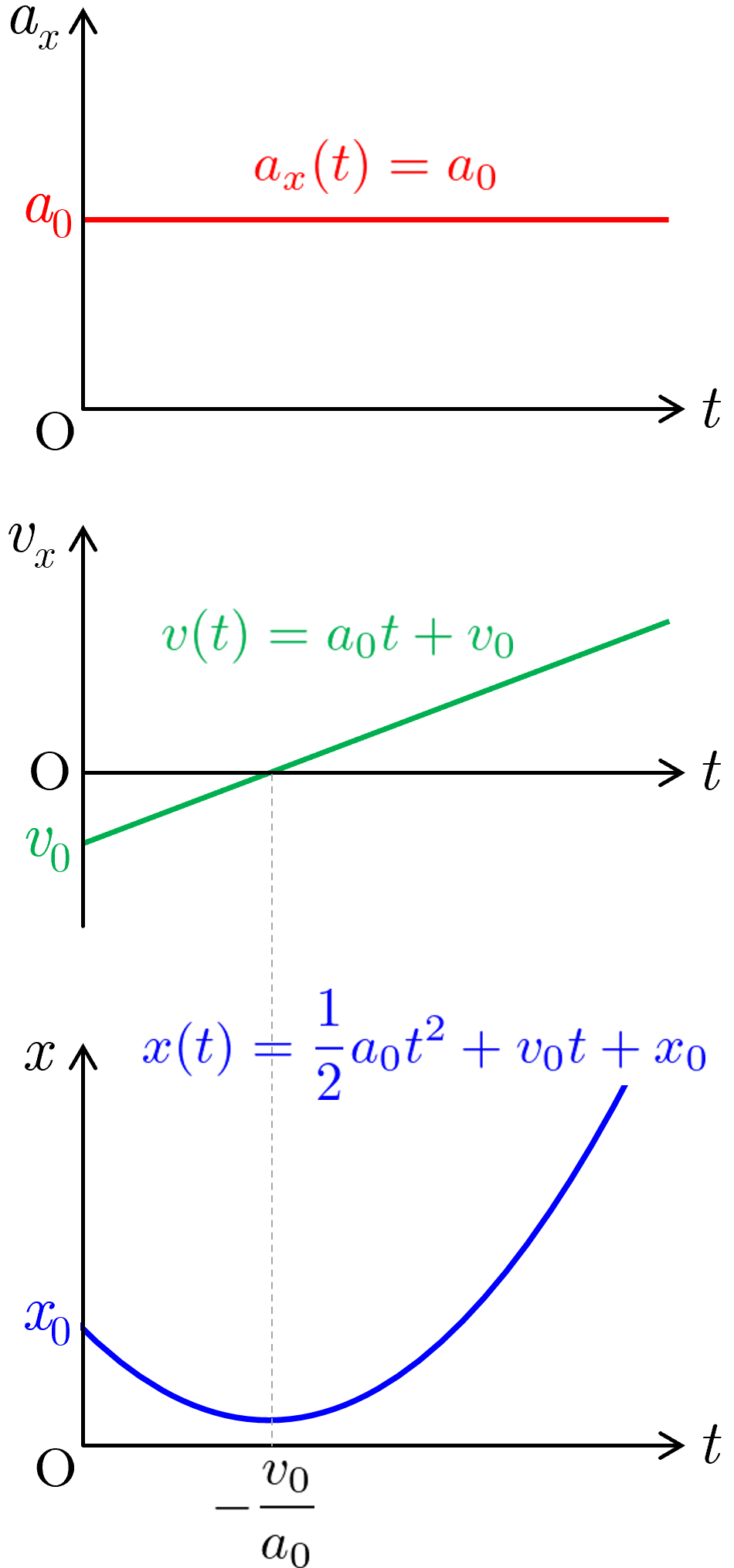
等加速度直線運動の
グラフ(上)
グラフ(中)
グラフ(下)
物体の加速度 が時刻 に依らず一定の値 () とする.ここで,物体の質量を ,物体に作用する一定の力を とすると, である.物体の速度を として
(一定) --- (1)
であるので,両辺を時刻 で積分することにより,物体の速度が時刻 の関数として
と求まる( :積分定数).初速度(時刻 での速度)を とすると なので
--- (2)
である.さらに,物体の位置を として,上式の両辺を時刻 で積分すると,物体の位置が時刻 の関数として
と求まる( :積分定数).初期位置(時刻 での位置)を とすると なので
--- (3)
である.等加速度運動の例としては,物体が動摩擦力を受けながら滑る運動や,地表において重力のみが作用する運動などがある.
式(2),(3)から時刻 を消去すると,
--- (4)
の関係式が得られる.ここで, は, と同じ向きの単位ベクトルである.
【式(4)の導出】
式(2)右辺の を左辺に移項して,両辺ともに との内積をとると
⇒
が得られる.また,式(3)についても右辺の を左辺に移項して,両辺ともに との内積をとり,上で求めた の表式を代入すると
が得られ,式(4)が求まる.
もし,初速度 が加速度 と平行もしくはゼロならば,物体は等加速度で1次元の運動をする(等加速度直線運動).この場合,初期位置 を通って,加速度 と平行になるように 軸をとると,物体の速度と位置は
--- (5)
--- (6)
のように1次元の運動として表せる.ここで, は 軸上にある初期位置であり, , はそれぞれ,加速度と初速度の 方向成分を表す.つまり, 軸の正方向の単位ベクトルを として, , と表される.位置 は時刻 についての2次関数であり,平方完成すると
--- (7)
となって, グラフの頂点 が
--- (8)
であることが分かる.また,等加速度直線運動の場合,式(4)は
--- (9)
と表され,よく知られた関係式となる(式(5),(6)から を消去すれば容易に求められる).