位置 (position)

物体の位置を表す場合，その物体が存在する空間において，なんらかの座標系を考えて，その座標値を用いる必要がある．2次元および3次元空間の場合，一般的には，座標軸が互いに直交した直交座標系がよく用いられる．位置の単位は，その座標値の単位を用いて表す．

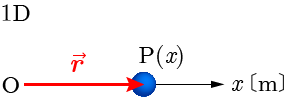
1次元空間（直線上）において，物体が ${\displaystyle x}$ 軸上の点Pに存在する場合（図を参照），その物体の位置は原点Oから測った ${\displaystyle x}$ 座標の値によって  ${\displaystyle (x)}$  のように表す．

原点Oを始点とし物体の位置Pを終点とするベクトルを位置ベクトルといい，1次元の場合  ${\displaystyle \overrightarrow{r}=(x)〔\text{m}〕}$  と表す．そのベクトルの大きさは

${\displaystyle r=\text{|}\overrightarrow{r}\text{|}=\left|x\right|〔\text{m}〕}$

で与えられ，原点からの距離を表す．

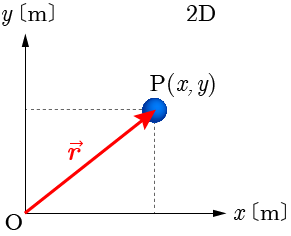
2次元空間において図のような直交座標系を考えた場合，点Pに存在する物体の位置は， ${\displaystyle x}$ 座標の値と ${\displaystyle y}$ 座標の値を用いて  ${\displaystyle (x,y)}$  のように表される．

位置ベクトルは平面ベクトルであり，   ${\displaystyle \overrightarrow{r}=(x,y)〔\text{m}〕}$  と表され，そのベクトルの大きさは

${\displaystyle r=\text{|}\overrightarrow{r}\text{|}=\sqrt{x^2+y^2}〔\text{m}〕}$

で与えられる．

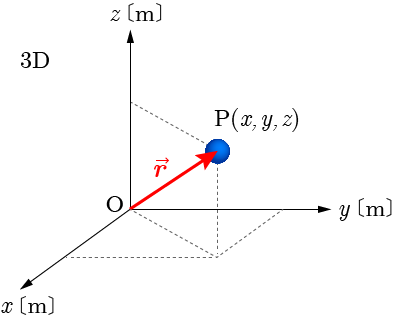
3次元空間において図のような直交座標系を考えた場合，点Pに存在する物体の位置は， ${\displaystyle x}$ 座標， ${\displaystyle y}$ 座標， ${\displaystyle z}$ 座標の値を用いて  ${\displaystyle (x,y,z)}$  のように表される．

位置ベクトルは空間ベクトルであり，   ${\displaystyle \overrightarrow{r}=(x,y,z)〔\text{m}〕}$  と表され，そのベクトルの大きさは

${\displaystyle r=\text{|}\overrightarrow{r}\text{|}=\sqrt{x^2+y^2+z^2}〔\text{m}〕}$

で与えられる．

座標系には，直交座標系以外にも，極座標系，斜交座標系，球面座標系などがあり，用途に応じて使い分けられている．

ホーム>>物理基礎>>第1編 物体の運動とエネルギー>>第1章　物体の運動>>位置

学生スタッフ作成
最終更新日： 2025年9月18日

[ページトップ]

利用規約

google translate (English version)