等加速度運動の導出（グラフから求める） (derivation of motion expression from graph)

時刻 ${\displaystyle t〔\mathrm{s}〕}$ での位置，速度，加速度をそれぞれ ${\displaystyle x\left(t\right)〔\text{m}〕}$  ， ${\displaystyle v\left(t\right)〔\text{m}/\text{s}〕}$  ， ${\displaystyle a\left(t\right)〔\text{m}/{\text{s}}^2〕}$   とする．

物体が等加速度直線運動をしているとき，物体の加速度は一定 ( ${\displaystyle a=\text{const}}$ )である．

初期条件：時刻 ${\displaystyle t=0\text{s}}$   での速度を ${\displaystyle v(0)=v_0〔\text{m}/\text{s}〕}$   ，位置を ${\displaystyle x(0)=x_0〔\text{m}〕}$   とする．

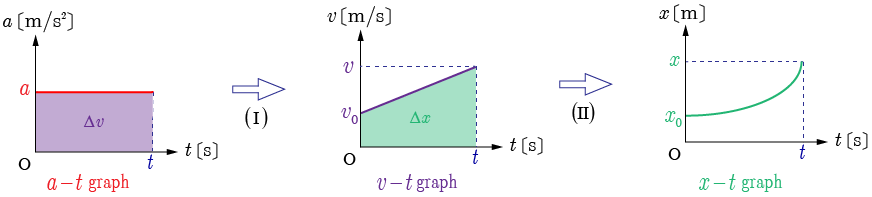
${\displaystyle \left(\mathrm{I}\right)}$ ${\displaystyle a-t}$グラフの水色の部分の面積は${\displaystyle 0\sim t}$ 秒間の速度の増加量 ${\displaystyle \Delta v〔\text{m}/\text{s}〕}$ を示し

${\displaystyle \Delta v=at}$

よって時刻 ${\displaystyle t〔\mathrm{s}〕}$ での速度は，

${\displaystyle v=v_0+\Delta v=v_0+at}$

と表される．

${\displaystyle \left(\mathrm{II}\right)}$ ${\displaystyle v-t}$グラフの水色の部分の面積は ${\displaystyle 0\sim t}$ 秒間の位置の増加量 ${\displaystyle \Delta x〔\text{m}〕}$を示し

${\displaystyle \Delta x=\frac{v+v_0}{2}t=\frac{v_0+at+v_0}{2}t=v_{0}t+\frac{1}{2}a{t}^2}$

よって時刻 ${\displaystyle t〔\mathrm{s}〕}$ での位置は，

${\displaystyle x=x_0+\Delta x=x_0+v_{0}t+\frac{1}{2}a{t}^2}$

と表される．

詳細

ホーム>>物理基礎>>第1編 物体の運動とエネルギー>>第1章　物体の運動>>等加速度運動の導出（グラフから求める）

学生スタッフ作成

最終更新日： 2025年9月19日