ヤングの実験と類似の実験
以下に,ヤングの干渉実験に類似した実験を紹介する.
(a) ロイドの鏡
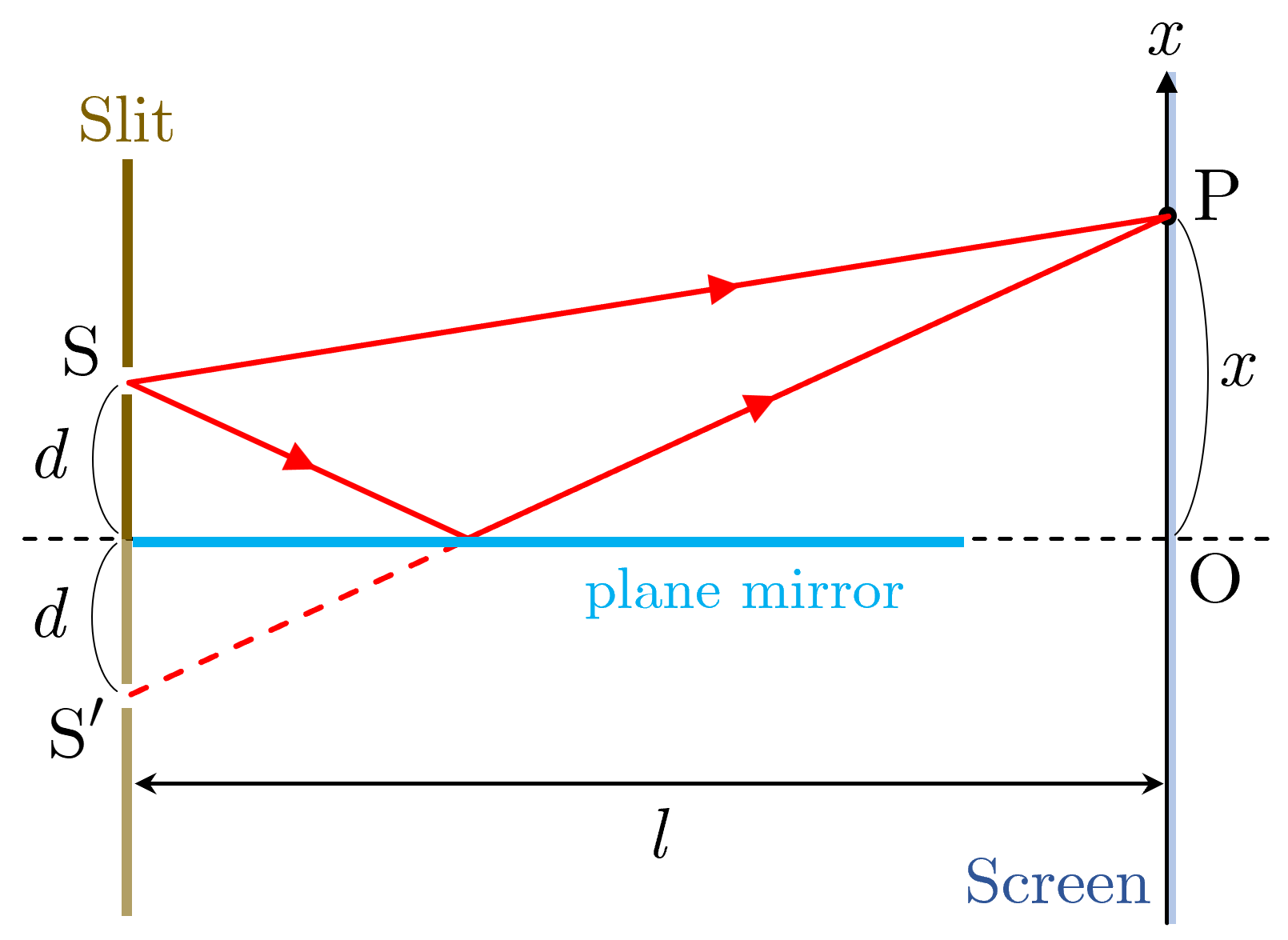
図1
図1のように,光源 から直接,スクリーン上の点 に達する光と,平面鏡で反射して点 に達する光の干渉により,明暗の縞模様ができる.平面鏡での反射による光源 の像を とすると,スリットの間隔が のヤングの実験と同じになる.ただし,鏡の反射で光波の位相が だけずれるので,干渉縞の条件式は明暗が逆になる.
(b) フレネルの2面鏡
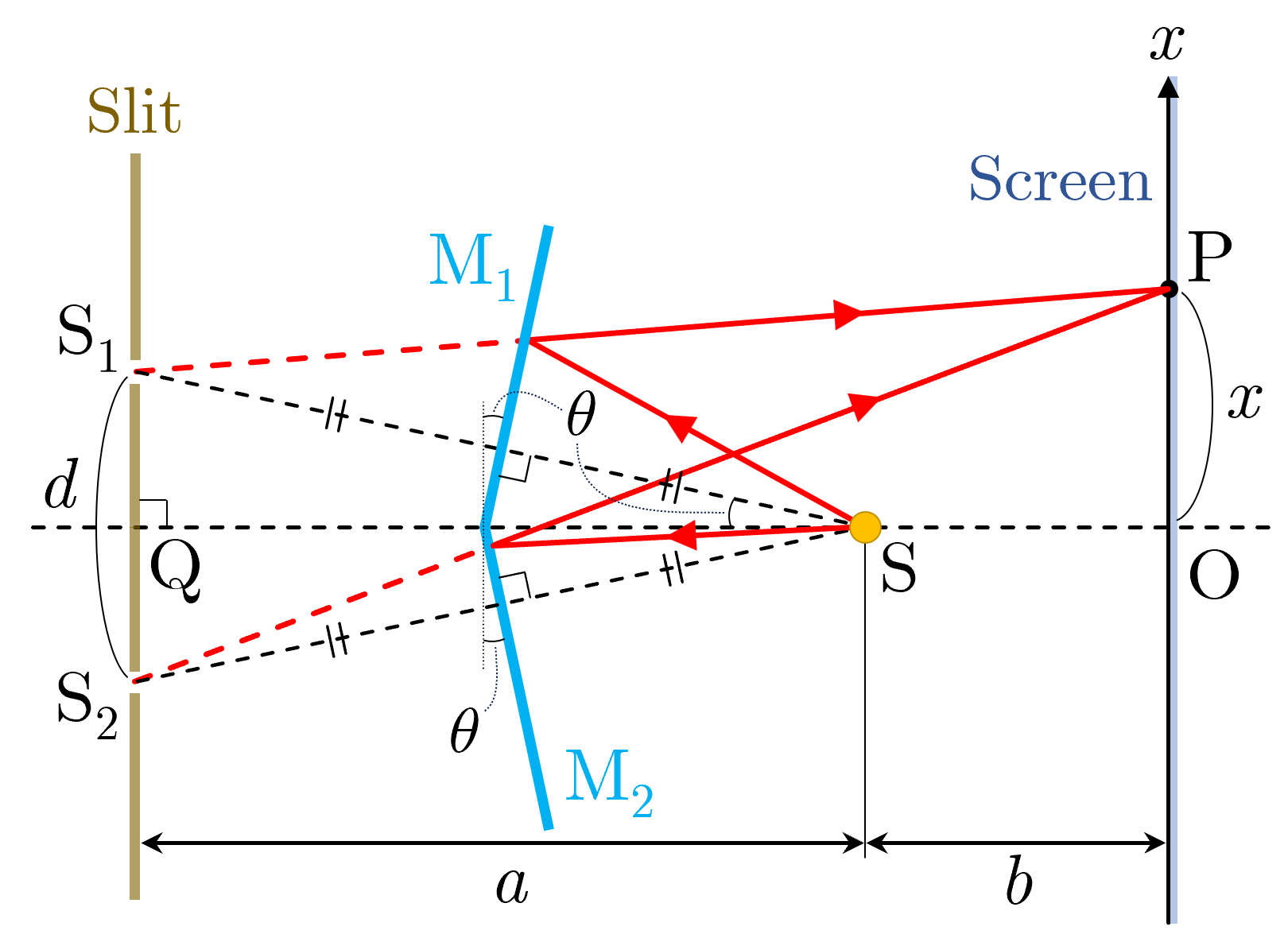
図2
図2のように,極めて小さい角 だけ傾いた2枚の鏡 , の前方の光源 から出た光の反射光は , の像 , から出たかのように反射してスクリーン上に干渉縞を形成する. , がヤングの実験における複スリットに相当する. より と近似できるので,図2より,この仮想的な複スリットの間隔 は
となる.複スリットからスクリーンまでの距離は であるので,光源の波長を とすると,明線の間隔 は
と表される.
(c) フレネルの複プリズム
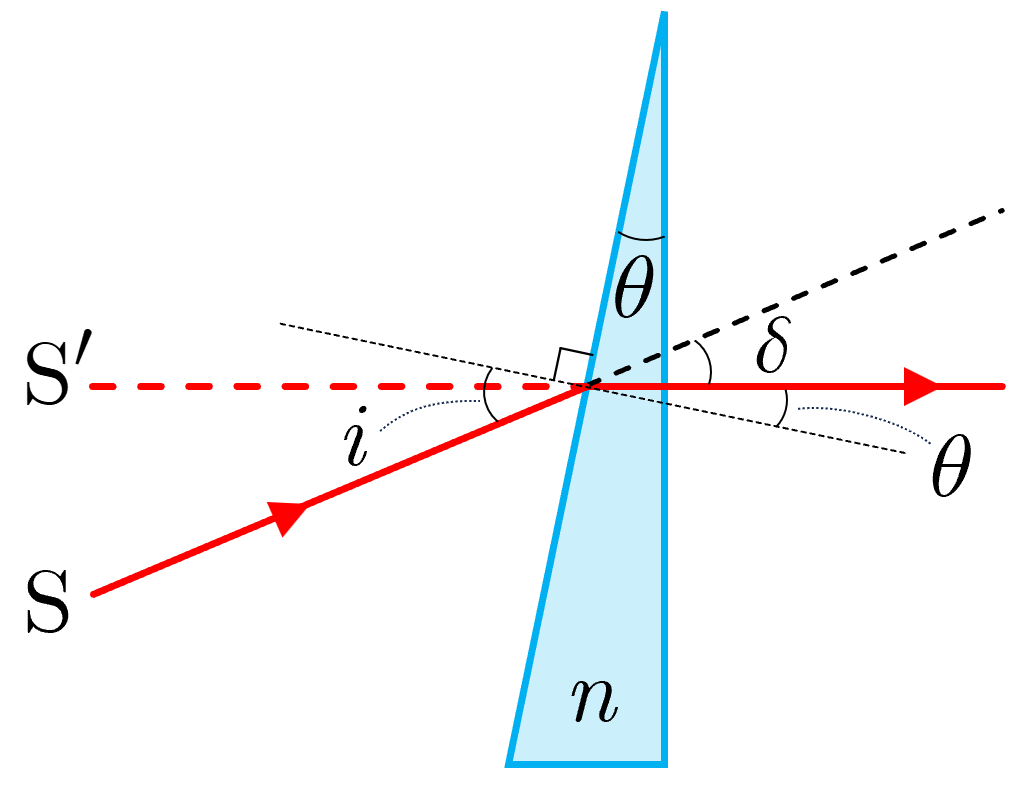
図3
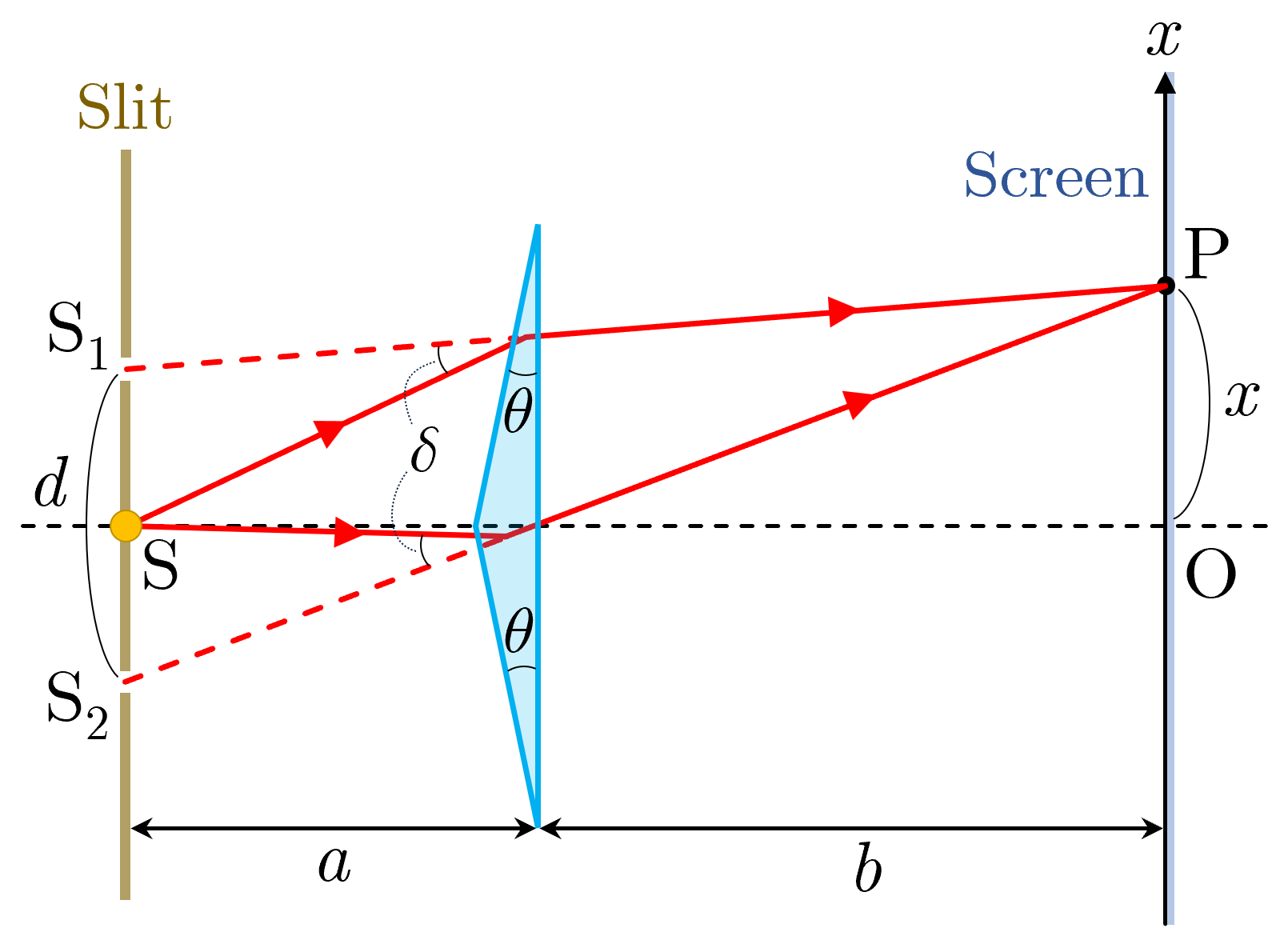
図4
図3のように,屈折率 ,小さな頂角 のプリズムに,小さい入射角 で入射した光と透過光との振れの角度を とする. , より, , と近似でき,屈折の法則 から となる.また, なので
と表せる.図3では,透過光がプリズムの右側の面と垂直をなしている場合を示しているが,そうでない場合もこの近似式は成り立つ.
図4のように,小さな頂角 の2つのプリズムを面対称に貼り合わせたものに波長 の光を当てるとスクリーン上に干渉縞を生じる.光源 から出た光はすべて振れの角 だけ進路を変えて透過するので,あたかも , から出た光のように直進する. より を用いると,
なので,明線の間隔 は
と表される.
ホーム>>物理>>第3編 波>>第3章 光>>ヤングの実験と類似の実験
学生スタッフ作成
最終更新日: 2025年10月24日