第2次導関数まで増減表に関する問題

■問題

関数 ${\displaystyle f\left(x\right)=e^{-x^2}}$ の第2次導関数までの増減表を作成し，極値と変曲点を求めよ．

■答

関数

${\displaystyle f\left(x\right)=e^{-x^2}}$ 　･･････(1)

の導関数を求める．

${\displaystyle f{\left(x\right)}^{\prime }=e^{-x^2}{\left(-x^2\right)}^{\prime }=-2x{e}^{-x^2}}$ 　･･････(2)

第2次導関数を求める．

${\displaystyle f{\left(x\right)}^{″}={\left(-2x\right)}^{\prime }{e}^{-x^2}-2x{\left(e^{-x^2}\right)}^{\prime }}$

${\displaystyle =-2e^{-x^2}-2x\left(-2x{e}^{-x^2}\right)}$

${\displaystyle =-2e^{-x^2}+4x^2{e}^{-x^2}}$

${\displaystyle =2e^{-x^2}\left(2x^2-1\right)}$　･･････(3)

${\displaystyle f^{\prime }\left(x\right)=0}$ となる $x$ の値を求める.

${\displaystyle f{\left(x\right)}^{\prime }=-2x{e}^{-x^2}=0}$

${\displaystyle e^{-x^2}>0}$

よって

${\displaystyle x=\mathrm{０}}$

となる．

${\displaystyle f^{″}\left(x\right)=0}$ となる $x$ の値を求める．

${\displaystyle f{\left(x\right)}^{\prime \text{}\prime }=2e^{-x^2}\left(2x^2-1\right)=0}$

${\displaystyle e^{-x^2}>0}$

よって

${\displaystyle 2x^2-1=0}$ ，${\displaystyle x=\pm \frac{1}{\sqrt{2}}}$

となる．

${\displaystyle f\left(-\frac{1}{\sqrt{2}}\right)=e^{-{\left(-\frac{1}{\sqrt{2}}\right)}^2}}$ ${\displaystyle =e^{-\frac{1}{2}}}$ ${\displaystyle =\frac{1}{\sqrt{e}}}$

${\displaystyle f\left(0\right)=e^{-0^2}=e^0=1}$

${\displaystyle f\left(\frac{1}{\sqrt{2}}\right)=e^{-{\left(\frac{1}{\sqrt{2}}\right)}^2}}$ ${\displaystyle =e^{-\frac{1}{2}}}$ ${\displaystyle =\frac{1}{\sqrt{e}}}$

${\displaystyle \underset{x\to \pm \infty }{\lim }f\left(x\right)=\underset{x\to \pm \infty }{\lim }{e}^{-x^2}}$ ${\displaystyle =\underset{x\to \pm \infty }{\lim }\frac{1}{e^{x^2}}=0}$

以上より，増減表を作成する．

増減表より

$x=0$ のとき極大値 $1$， 変曲点 ${\displaystyle \left(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{e}}\right)}$ と ${\displaystyle \left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{e}}\right)}$

となる．

●参考

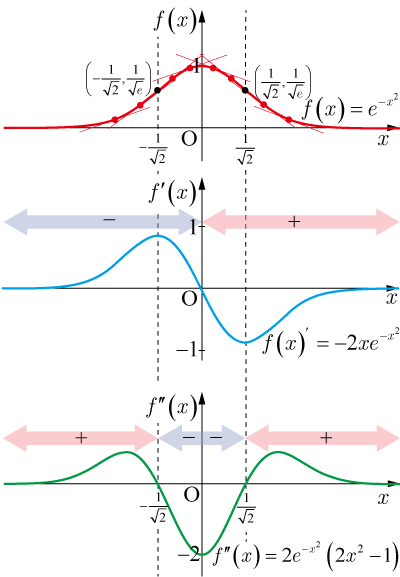
増減表と対比できるように $f\left(x\right)$ ， $f^{\prime }\left(x\right)$ ， $f^{″}\left(x\right)$ のグラフを示す．

　

ホーム>>カテゴリー分類>>微分>>微分に関する演習問題>>極値の問題>>第2次導関数まで増減表に関する問題

最終更新日： 2025年4月27日