円の方程式

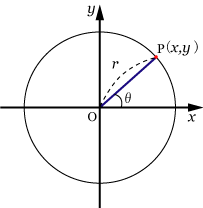中心：原点，半径：r の円の方程式
中心：C(a,b)，半径：r の円の方程式
原点Oと点Q(a,b)を結ぶ直線OPを直径とする円の方程式
複素数を用いた円の方程式
ベクトルを用いた円の方程式

■中心：原点，半径：r の円の方程式

$3$ {x}^{2}+{y}^{2}={r}^{2}$

$3$\displaystyle{r}$ と $3$\displaystyle{{\theta}}$ を使って円周上の点Pを表すと

$3$\displaystyle{ \{\begin{array}{lll}x=r\cos {\theta}& \vspace{6}\\ y=r\sin {\theta}& \vspace{6}\\ \end{array} }$

となる．

$3$\displaystyle{\begin{array}{lll} {x}^{2}+{y}^{2} & ={ $ r\cos {\theta} $ }^{2}+{ $ r\sin {\theta} $ }^{2} & \vspace{6}\\ & ={r}^{2} $ { \cos }^{2}{\theta}+{ \sin }^{2}{\theta} $ & \vspace{6}\\ & ={r}^{2} & \vspace{6}\\ \end{array}}$

■中心：C(a,b)，半径：r の円の方程式[topへ]

$3${ $ x- a $ }^{2}+{ $ y- b $ }^{2}={r}^{2}$

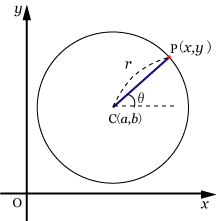
$3$\displaystyle{r}$ と $3$\displaystyle{{\theta}}$ を使って円周上の点Pを表すと

$3$\displaystyle{ \{\begin{array}{lll}x=a+r\cos {\theta}& \vspace{6}\\ y=b+r\sin {\theta}& \vspace{6}\\ \end{array} }$

となる．

$3$\displaystyle{ { $ x- a $ }^{2}+ { $ y- b $ }^{2} }$ $3$\displaystyle{ ={ $ a+ r\cos {\theta}- a $ }^{2}+ { $ b+ r\sin {\theta}- b $ }^{2} }$

■原点Oと点Q(a,b)を結ぶ直線OPを直径とする円の方程式[topへ]

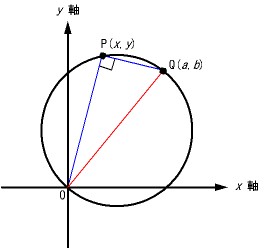
$3$\displaystyle{{ $ x- \frac{\hspace{2}a\hspace{2}}{\hspace{2}2\hspace{2}} $ }^{2}+{ $ y- \frac{\hspace{2}b\hspace{2}}{\hspace{2}2\hspace{2}} $ }^{2}=\frac{\hspace{2} {a}^{2}+{b}^{2} \hspace{2}}{\hspace{2}4\hspace{2}}}$

●式の導出その1

　円周角の定理より $3$\angle \text{OPQ}=90^\circ$ ．
よって， $3$\displaystyle{ { \text{OP} }\limits^{\longrightarrow } }$ , $3$\displaystyle{ { \text{QP} }\limits^{\longrightarrow } }$ の内積は， $3${ \text{OP} }\limits^{\longrightarrow }\cdot { \text{QP} }\limits^{\longrightarrow }=0$ となる．
この関係を，ベクトルの成分で表すと

$3${ \text{OP} }\limits^{\longrightarrow }= $ x,y $ ,{ \text{QP} }\limits^{\longrightarrow }= $ x- a,y- b $$

より

$3$x $ x- a $ +y $ y- b $ =0$

となる．上記のような円の方程式の形に変形すると

となる．

　これが求める円の方程式である．

中心の座標は， $3$\displaystyle{ $ \frac{\hspace{2}a\hspace{2}}{\hspace{2}2\hspace{2}},\frac{\hspace{2}b\hspace{2}}{\hspace{2}2\hspace{2}} $ }$ ，半径は， $3$\displaystyle{\frac{\hspace{2} \sqrt{ {a}^{2}+{b}^{2} } \hspace{2}}{\hspace{2}2\hspace{2}}}$ となる．

　内積を用いて円の方程式を導く方法は重要である．

●式の導出その2

　三平方の定理を用いて方程式を導くこともできます．

$3$\displaystyle{{\text{OQ}}^{2}={\text{OP}}^{2}+{\text{QP}}^{2}}$ より

$3$\displaystyle{ {a}^{2}+ {b}^{2} }$ $3$\displaystyle{ ={x}^{2}+ {y}^{2}+ { $x- a$ }^{2}+ { $ y- b $ }^{2} }$

$3$\displaystyle{ {a}^{2}+ {b}^{2} }$ $3$\displaystyle{ ={x}^{2}+ {y}^{2}+ {x}^{2}- 2ax+ {a}^{2}+ {y}^{2}- 2by+ {b}^{2} }$

$3$\displaystyle{ 0=2 $ {x}^{2}- ax+ {y}^{2}- by $ }$

$3$\displaystyle{ {x}^{2}- ax+ {y}^{2}- by=0 }$

$3$\displaystyle{ { $ x- \frac{\hspace{2}a\hspace{2}}{\hspace{2}2\hspace{2}} $ }^{2}+ { $ y- \frac{\hspace{2}b\hspace{2}}{\hspace{2}2\hspace{2}} $ }^{2}=\frac{\hspace{2} {a}^{2}+ {b}^{2} \hspace{2}}{\hspace{2}4\hspace{2}} }$

■複素数を用いた円の方程式[topへ]

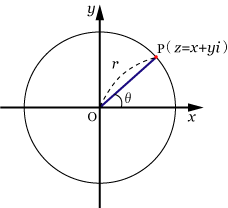● 複素平面上において，原点Oを中心とする半径 $3$\displaystyle{r}$ の円の方程式

　複素数を $3$\displaystyle{ z=x+yi }$ とすると

$3$\displaystyle{ \|z\| =r }$ （ $3$\displaystyle{ r=\sqrt{ {x}^{2}+{y}^{2} } }$ ）

極形式で表すと

$3$\displaystyle{z=r $ \cos {\theta}+i\sin {\theta} $ }$

となる．

● 複素平面上において，点C（ $3$\displaystyle{{\alpha}=a+bi}$ ）を中心とする半径 $3$\displaystyle{r}$ の円の方程式

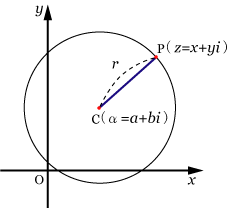複素数を $3$\displaystyle{ z=x+yi }$ とすると

$3$\displaystyle{ \mid z- {\alpha} \mid =r }$

$3$\displaystyle{ \mid $ x- yi $ - $ a+ bi $ \mid =r }$

$3$\displaystyle{ \mid $ x- a $ + $ y- b $ i \mid =r }$

ただし， $3$\displaystyle{ $ r=\sqrt{ { \( x- a $ }^{2}+ { $ y- b $ }^{2} } \) }$

となる．

● 複素平面において，点A（ $3$\displaystyle{ {\alpha}=a+bi }$ ）と点B（ $3$\displaystyle{{\beta}=c+di}$ ）があり，線分ABを直径とする円の方程式

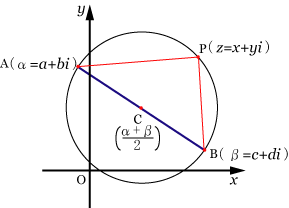　複素数を $3$\displaystyle{ z=x+yi }$ とすると

$3$\displaystyle{arg\frac{\hspace{2} z- {\alpha} \hspace{2}}{\hspace{2} z- {\beta} \hspace{2}}=\pm 90^\circ }$

（円周角の定理と複素数平面での2直線のなす角を参照）

あるいは

円の中心が $3$\displaystyle{\frac{\hspace{2} {\alpha}+{\beta} \hspace{2}}{\hspace{2}2\hspace{2}}}$ ，円の半径が $3$\displaystyle{\frac{\hspace{2} \| {\alpha}- {\beta} \| \hspace{2}}{\hspace{2}2\hspace{2}}}$ となるので

$3$\displaystyle{ \| z- \frac{\hspace{2} {\alpha}+{\beta} \hspace{2}}{\hspace{2}2\hspace{2}} \| =\frac{\hspace{2} \| {\alpha}- {\beta} \| \hspace{2}}{\hspace{2}2\hspace{2}}}$

と表すこともできる．

■ベクトルを用いた円の方程式[topへ]

●原点が中心で半径 $3$r$ の円の方程式

円周上の点 $3$\text{P}$ の位置ベクトルを $3$\displaystyle{{p}\limits^{\rightarrow }=\left({ x,y }\right)}$ とすると，円の方程式は

$3$\displaystyle{\left|{{p}\limits^{\rightarrow }}\right|=r}$ 　⇒ 導出

となる．

●点 $3$\text{C}$ $3$\displaystyle{\left({ a,b }\right)}$ が中心で半径 $3$r$ の円の方程式

円周上の点 $3$\text{P}$ の位置ベクトルを $3$\displaystyle{{p}\limits^{\rightarrow }=\left({ x,y }\right)}$ ，点 $3$\text{C}$ の位置ベクトルを $3$\displaystyle{{c}\limits^{\rightarrow }=\left({ a,b }\right)}$ とすると，円の方程式は

$3$\displaystyle{\left|{ {p}\limits^{\rightarrow }- {c}\limits^{\rightarrow } }\right|=r}$ 　⇒ 導出

となる．

●点 $3$\text{A}$ $3$\displaystyle{\left({ \hspace{1}{x}_{a},\hspace{1}{y}_{a} }\right)}$ ，点 $3$\text{B}$ $3$\displaystyle{\left({ \hspace{1}{x}_{b},\hspace{1}{y}_{b} }\right)}$ において，線分 $3$\text{AB}$ を直径とする円の方程式

円周上の点 $3$\text{P}$ の位置ベクトルを $3$\displaystyle{{p}\limits^{\rightarrow }=\left({ x,y }\right)}$ ，点 $3$\text{A}$ の位置ベクトルを $3$\displaystyle{{a}\limits^{\rightarrow }=\left({ \hspace{1}{x}_{a},\hspace{1}{y}_{a} }\right)}$ ，点 $3$\text{B}$ の位置ベクトルを $3$\displaystyle{{b}\limits^{\rightarrow }=\left({ \hspace{1}{x}_{b},\hspace{1}{y}_{b} }\right)}$ とすると，円の方程式は

$3$\displaystyle{\left({ {p}\limits^{\rightarrow }- {a}\limits^{\rightarrow } }\right)\cdot \left({ {p}\limits^{\rightarrow }- {b}\limits^{\rightarrow } }\right)=0}$ 　⇒ 導出

となる．

ホーム>>カテゴリー分類>>関数>>円の方程式

最終更新日： 2025年10月15日

円の方程式

■中心：原点，半径：r の円の方程式

■中心：C(a,b)，半径：r の円の方程式[topへ]

■原点Oと点Q(a,b)を結ぶ直線OPを直径とする円の方程式[topへ]

●式の導出 その1

●式の導出 その2

■複素数を用いた円の方程式[topへ]

● 複素平面上において，原点Oを中心とする半径 の 円の方程式

● 複素平面上において，点C（ ）を中心とする半径 の 円の方程式

● 複素平面において，点A（ ）と点B（ ）があり，線分ABを直径とする円の方程式

■ベクトルを用いた円の方程式[topへ]

●原点が中心で半径 の円の方程式

●点 が中心で半径 の円の方程式

●点 ，点 において，線分 を直径とする円の方程式

●式の導出その1

●式の導出その2

● 複素平面上において，原点Oを中心とする半径 $3$\displaystyle{r}$ の円の方程式

● 複素平面上において，点C（ $3$\displaystyle{{\alpha}=a+bi}$ ）を中心とする半径 $3$\displaystyle{r}$ の円の方程式

● 複素平面において，点A（ $3$\displaystyle{ {\alpha}=a+bi }$ ）と点B（ $3$\displaystyle{{\beta}=c+di}$ ）があり，線分ABを直径とする円の方程式

●原点が中心で半径 $3$r$ の円の方程式

●点 $3$\text{C}$ $3$\displaystyle{\left({ a,b }\right)}$ が中心で半径 $3$r$ の円の方程式

●点 $3$\text{A}$ $3$\displaystyle{\left({ \hspace{1}{x}_{a},\hspace{1}{y}_{a} }\right)}$ ，点 $3$\text{B}$ $3$\displaystyle{\left({ \hspace{1}{x}_{b},\hspace{1}{y}_{b} }\right)}$ において，線分 $3$\text{AB}$ を直径とする円の方程式