不等式と領域

■1次関数と不等式

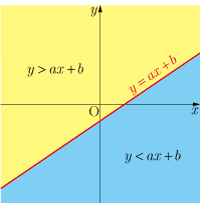
不等式 $y > a x + b$ を満たす点 $(x, y)$ の集合の領域は， $x y$ 座標平面に描かれた直線 $y = a x + b$ より $y$ の値が大きくなっている領域(直線より上の領域)になる（図の黄色の領域）．

不等式 $y < a x + b$ を満たす点 $(x, y)$ の集合の領域は， $x y$ 座標平面に描かれた直線 $y = a x + b$ より $y$ の値が小さくなっている領域(直線より下の領域)になる（図の青色の領域）．

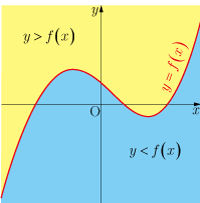
不等式 $y > f (x)$ を満たす点 $(x, y)$ の集合の領域は， $x y$ 座標平面に描かれた曲線 $y = f (x)$ より $y$ の値が大きくなっている領域(曲線より上の領域)になる（図の黄色の領域）．

不等式 $y < f (x)$ を満たす点 $(x, y)$ の集合の領域は， $x y$ 座標平面に描かれた曲線 $y = f (x)$ より $y$ の値が小さくなっている領域(曲線より下の領域)になる（図の青色の領域）．

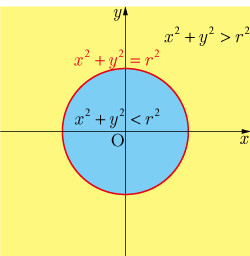
不等式 $x^{2} + y^{2} > r^{2}$ を満たす点 $(x, y)$ の集合の領域は， $x y$ 座標平面に描かれた円 $x^{2} + y^{2} = r^{2}$ より外側の領域になる（図の黄色の領域）．

不等式 $x^{2} + y^{2} < r^{2}$ を満たす点 $(x, y)$ の集合の領域は， $x y$ 座標平面に描かれた円 $x^{2} + y^{2} = r^{2}$ より内側の領域になる（図の青色の領域）．

上記で取り扱った不等式を以下のように書き変える．

$y > a x + b$ 　⇒　 $y - (a x + b) > 0$

$y < a x + b$ 　⇒　 $y - (a x + b) < 0$

$y > f (x)$ 　⇒　 $y - f (x) > 0$

$y < f (x)$ 　⇒　 $y - f (x) < 0$

$x^{2} + y^{2} > r^{2}$ 　⇒　 $x^{2} + y^{2} - r^{2} > 0$

$x^{2} + y^{2} < r^{2}$ 　⇒　 $x^{2} + y^{2} - r^{2} < 0$

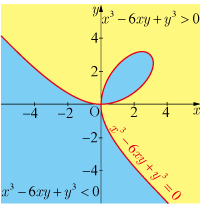
不等式の左辺の関数を一般化すると $x$ と $y$ の2変数関数 $f (x, y)$ を用いて表現することができきる．

$f (x, y) = 0$ で表される陰関数の曲線が領域の境界線となり

不等式 $f (x, y) > 0$ を満たす点 $(x, y)$ の集合の領域を $f (x, y)$ の正領域

不等式 $f (x, y) < 0$ を満たす点 $(x, y)$ の集合の領域を $f (x, y)$ の負領域

という．

最終更新日： 2024年6月20日