空間における直線の方程式

点$\text{P}$ $\left(x_0,y_0,z_0\right)$ を通り，方向ベクトルが $\overrightarrow{d}=\left(l,m,n\right)$ の直線の方程式は

${\displaystyle \frac{x-x_0}{l}=\frac{y-y_0}{m}=\frac{z-z_0}{n}}$

と表わされる．また，媒介変数（パラメーター） $t$を用いて表すと

$x=x_0+tl$ ，$y=y_0+tm$ ，$z=z_0+tn$

と表される．このような直線の方程式の表現方法を媒介変数表示という．

座標平面での直線の方程式はここを参照．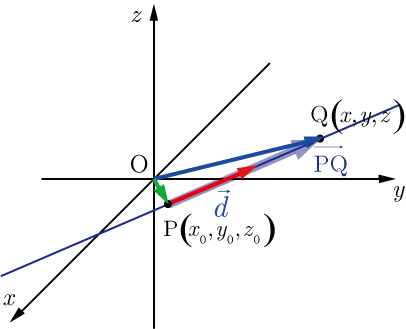

■直線の方程式の導出

直線は，空間（座標空間）中の点と方向ベクトルが決まれば，一意的に決まる．空間中の点$\text{P}$ の座標を ${\displaystyle \left(x_0,y_0,z_0\right)}$ ，方向ベクトルを ${\displaystyle \overrightarrow{d}=\left(l,m,n\right)}$  とし，直線上の点$\text{Q}$ の座標を${\displaystyle \left(x,y,z\right)}$  とすると

${\displaystyle \stackrel{⟶}{\text{PQ}}=t\overrightarrow{d}}$   （t は媒介変数）

となるので

${\displaystyle \overrightarrow{\text{OQ}}=\overrightarrow{\text{OP}}+\overrightarrow{\text{PQ}}}$${\displaystyle =\overrightarrow{\text{OP}}+t\overrightarrow{d}}$

と表すことができる．これをベクトルの成分表示で表すと

${\displaystyle \left(x,y,z\right)=\left(x_0,y_0,z_0\right)+t\left(l,m,n\right)}$

あるいは

${\displaystyle \{\begin{array}{l}x=x_0+tl\\ y=y_0+tm\\ z=z_0+tn\end{array}}$  

となり，媒介変数を用いた直線の方程式が求まる．次に媒介変数 t の消去を図る．

${\displaystyle \begin{array}{lll}x=x_0+tl\hfill & \to \hfill & t={\displaystyle \frac{x-x_0}{l}}\hfill \\ y=y_0+tm\hfill & \to \hfill & t={\displaystyle \frac{y-y_0}{m}}\hfill \\ z=z_0+tn\hfill & \to \hfill & t={\displaystyle \frac{z-z_0}{n}}\hfill \end{array}}$

となり，t を消去すると

${\displaystyle \frac{x-x_0}{l}=\frac{y-y_0}{m}=\frac{z-z_0}{n}}$

となる．このように直線の方程式が求まる．

 

ホーム>>カテゴリー分類>>関数>>直線の方程式

最終更新日： 2024年12月5日