概念問題 解答

線形代数　行列

問題7の解答

原点を中心に反時計回りに $\theta$ 回転させる1次変換の表現行列（回転行列）は

${\displaystyle \left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)}$　･･････(1)

である．

原点を中心に時計回りに $\theta$ 回転させる1次変換の表現行列（回転行列）は

${\displaystyle \left(\begin{array}{cc}\cos \left(-\theta \right)& -\sin \left(-\theta \right)\\ \sin \left(-\theta \right)& \cos \left(-\theta \right)\end{array}\right)=\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)}$　･･････(2)

である．

●(1)，(2)より各選択肢が当てはまるかどうかを調べる．

1. (2)より，原点を中心に時計回りに $\theta$ 回転させる1次変換の表現行列である．よって，当てはまらない．
2. (1)より，原点を中心に反時計回りに $2\theta$ 回転させる1次変換の表現行列である．よって，当てはまらない．
3. (1)より，原点を中心に反時計回りに $\theta$ 回転させる1次変換の表現行列である．よって，当てはまらない．
4. (1)，(2)だだけではどのような変換の表現行列かは判定できない．

以上より，原点 $\text{O}$ を通り， $x$ 軸となす角が $\theta$ 〔°〕の直線に関して，対称な点に移す1次変換の表現行列は4であると推察できる．

●原点 $\text{O}$ を通り， $x$ 軸となす角が $\theta$ 〔°〕の直線に関して，対称な点に移す1次変換の表現行列を求める．

点 $\text{P}$ の座標を ${\displaystyle \left(\begin{array}{c}x\\ y\end{array}\right)}$ ， 点 $\text{Q}$ の座標を ${\displaystyle \left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)}$ とする．

点 $\text{P}$ と点 $\text{Q}$ が $x$ 軸となす角が $\theta$ 〔°〕の直線に関して対称であることより

1. 点 $\text{P}$ と点 $\text{Q}$ の中点が $x$ 軸となす角が $\theta$ 〔°〕の直線 （${\displaystyle y=\left(\tan \theta \right)x}$ ）にある．よって

   ${\displaystyle \frac{y+y^{\prime }}{2}=\left(\tan \theta \right)\frac{x+x^{\prime }}{2}}$　･･････(3)

2. 線分 $\text{PQ}$ と直線 ${\displaystyle y=\left(\tan \theta \right)x}$ が直交する．よって

   ${\displaystyle \frac{y^{\prime }-y}{x^{\prime }-x}\cdot \tan \theta =-1}$　･･････(4)

   ここで， ${\displaystyle \frac{y^{\prime }-y}{x^{\prime }-x}}$ は線分 $\text{PQ}$ の傾き， $\tan \theta$ は直線 ${\displaystyle y=\left(\tan \theta \right)x}$ の傾きである．

となる．

(3)，(4)の連立方程式から， $x^{\prime }$ ， $y^{\prime }$ を $x$ ， $y$ で表すようにする．

(3)より

${\displaystyle y+y^{\prime }=\left(\tan \theta \right)\left(x+x^{\prime }\right)}$

${\displaystyle y+y^{\prime }=x\tan \theta +x^{\prime }\tan \theta }$　･･････(5)

(4)より

${\displaystyle y^{\prime }-y=\frac{-1}{\tan \theta }\left(x^{\prime }-x\right)}$

${\displaystyle y^{\prime }-y=-\frac{x^{\prime }}{\tan \theta }+\frac{x}{\tan \theta }}$　･･････(6)

(5)－(6)より（以下の計算では，2倍角の公式，三角関数の相互関係を用いて式を整理している）

${\displaystyle 2y=x\tan \theta +x^{\prime }\tan \theta +\frac{x^{\prime }}{\tan \theta }-\frac{x}{\tan \theta }}$

${\displaystyle 2y=x\left(\tan \theta -\frac{1}{\tan \theta }\right)+x^{\prime }\left(\tan \theta +\frac{1}{\tan \theta }\right)}$

${\displaystyle 2y=x\left(\frac{\sin \theta }{\cos \theta }-\frac{\cos \theta }{\sin \theta }\right)+x^{\prime }\left(\frac{\sin \theta }{\cos \theta }+\frac{\cos \theta }{\sin \theta }\right)}$

${\displaystyle 2y=x\left(\frac{{\sin }^2\theta -{\cos }^2\theta }{\sin \theta \cos \theta }\right)+x^{\prime }\left(\frac{{\sin }^2\theta +{\cos }^2\theta }{\sin \theta \cos \theta }\right)}$

${\displaystyle 2y=x\left(\frac{-\cos 2\theta }{\frac{1}{2}\sin 2\theta }\right)+x^{\prime }\left(\frac{1}{\frac{1}{2}\sin 2\theta }\right)}$

${\displaystyle 2y=-\frac{2x}{\tan 2\theta }+\frac{2x^{\prime }}{\sin 2\theta }}$

${\displaystyle y=-\frac{x}{\tan 2\theta }+\frac{x^{\prime }}{\sin 2\theta }}$

${\displaystyle y\sin 2\theta =-\frac{x\sin 2\theta }{\tan 2\theta }+x^{\prime }}$

${\displaystyle y\sin 2\theta =-x\cos 2\theta +x^{\prime }}$

${\displaystyle x^{\prime }=x\cos 2\theta +y\sin 2\theta }$　･･････(7)

(5)に(7)を代入する．

${\displaystyle y+y^{\prime }=x\tan \theta +\left(x\cos 2\theta +y\sin 2\theta \right)\tan \theta }$

${\displaystyle y+y^{\prime }=x\tan \theta +x\cos 2\theta \tan \theta +y\sin 2\theta \tan \theta }$

${\displaystyle y^{\prime }=x\tan \theta +x\cos 2\theta \tan \theta +y\sin 2\theta \tan \theta -y}$

${\displaystyle y^{\prime }=x\left(\tan \theta +\cos 2\theta \tan \theta \right)+y\left(\sin 2\theta \tan \theta -1\right)}$

${\displaystyle y^{\prime }=x\left(\frac{\sin \theta }{\cos \theta }+\left({\cos }^2\theta -{\sin }^2\theta \right)\frac{\sin \theta }{\cos \theta }\right)+y\left(2\sin \theta \cos \theta \frac{\sin \theta }{\cos \theta }-1\right)}$

${\displaystyle y^{\prime }=x\left(\frac{\sin \theta }{\cos \theta }+\left\{{\cos }^2\theta -\left(1-{\cos }^2\theta \right)\right\}\frac{\sin \theta }{\cos \theta }\right)+y\left(2{\sin }^2\theta -1\right)}$

${\displaystyle y^{\prime }=x\left(\frac{\sin \theta }{\cos \theta }+\sin \theta \cos \theta -\frac{\sin \theta }{\cos \theta }+\sin \theta \cos \theta \right)+y\left(2{\sin }^2\theta -1\right)}$

${\displaystyle y^{\prime }=x\cdot 2\sin \theta \cos \theta +y\left(1-{\cos }^2\theta +{\sin }^2\theta -1\right)}$

${\displaystyle y^{\prime }=x\sin 2\theta +y\left(-{\cos }^2\theta +{\sin }^2\theta \right)}$

${\displaystyle y^{\prime }=x\cdot \sin 2\theta -y\cos 2\theta }$　･･････(8)

(7)，(8)より

${\displaystyle \left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{c}x\cos 2\theta +y\sin 2\theta \\ x\cdot \sin 2\theta -y\cos 2\theta \end{array}\right)=\left(\begin{array}{cc}\cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)}$

よって，表現行列は

${\displaystyle \left(\begin{array}{cc}\cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{array}\right)}$

となる．したがって，答は4となる．

●線形写像の合成を用いて表現行列を求める

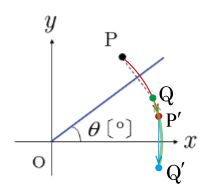
原点 $\text{O}$ を通り， $x$ 軸となす角が $\theta$ 〔°〕の直線に関して，対称な点に移す1次変換を3つの1次変換の合成と考える．図を参照のこと．

1. 点 $\text{P}$ を時計回りに $\theta$ 〔°〕回転させて，点 ${\text{P}}^{\prime }$ に移す．
2. 点 ${\text{P}}^{\prime }$ を $x$に関して対称な点 ${\text{Q}}^{\prime }$ に移す．
3. ${\text{Q}}^{\prime }$ を反時計回りに $\theta$ 〔°〕回転させて，点 $\text{Q}$ に移す．

点 ${\text{P}}^{\prime }$ の座標を ${\displaystyle \left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)}$ ， 点 ${\text{Q}}^{\prime }$ の座標を ${\displaystyle \left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)}$ とする．

点 $\text{P}$ を時計回りに $\theta$ 〔°〕回転させて，点 ${\text{P}}^{\prime }$ に移すことより

${\displaystyle \left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)=\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)}$　･･････(9)

が得られる．

∵(2)

点 ${\text{P}}^{\prime }$ を $x$に関して対称な点 ${\text{Q}}^{\prime }$ に移すことより

${\displaystyle \left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)}$　･･････(10)

∵この問題

が得られる．

${\text{Q}}^{\prime }$ を反時計回りに $\theta$ 〔°〕回転させて，点 $\text{Q}$ に移すことより

${\displaystyle \left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)}$　･･････(11)

∵(1)

が得られる．

(11)に(10)を代入する．

${\displaystyle \left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)}$　･･････(12)

(12)に(9)を代入する．

${\displaystyle \left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)}$

以下のように行列の計算をする．

${\displaystyle \left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{cc}\cos \theta & \sin \theta \\ \sin \theta & -\cos \theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)}$

${\displaystyle \left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}{\cos }^2\theta -{\sin }^2\theta & 2\sin \theta \cos \theta \\ 2\sin \theta \cos \theta & {\sin }^2\theta -{\cos }^2\theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)}$

${\displaystyle \left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)}$

よって，表現行列は

${\displaystyle \left(\begin{array}{cc}\cos 2\theta & \sin 2\theta \\ \sin 2\theta & -\cos 2\theta \end{array}\right)}$

となる．したがって，答は4となる．