「簡易単振り子」実験モジュール

※ 三角マークのついた項目をクリックすると説明文が現れる．

【実験の目的】

単振り子の長さと周期の2乗との間に線形関係がある（直線の式で表せる）ことを確かめ，その直線の傾きから重力加速度の大きさ $g$ の値を見積もる．

【原理・理論】

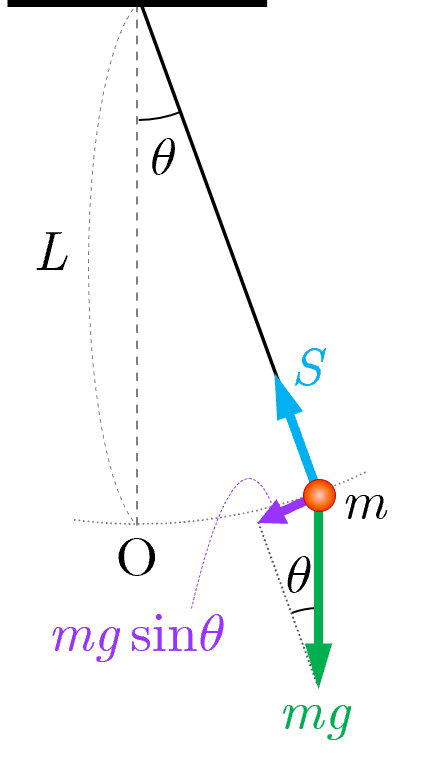
図のように，軽い糸の一端に質量 $m$ の小球をつけ，他端を支点に固定して振幅の小さな振動をさせる．ここで，小球の半径 $r$ と糸の長さ $l$ との和を単振り子の長さ $L$ $(= r + l)$ とし，重力加速度の大きさを $g$ とする．また，小球を吊るして静止させたときの小球の位置を点 $O$ として，小球はこの点 $O$ を通る鉛直平面内を振動し，空気の影響は無視できるものとする．

糸の鉛直方向となす角が $θ$ のとき，小球に作用する軌道の接線方向の力は $F = - m g \sin θ$ である．また，点 $O$ から小球までの円弧の長さは $L θ$ であるので，小球の加速度の接線方向成分は

$a = \frac{d^{2} (L θ)}{d t^{2}} = L \frac{d^{2} θ}{d t^{2}}$

となる．よって，小球の運動方程式は

$m L \frac{d^{2} θ}{d t^{2}} = - m g \sin θ$ ⇒ $\frac{d^{2} θ}{d t^{2}} = - \frac{g}{L} \sin θ$ ---- (1)

となる．振れ角が小さい場合， $\sin θ \approx θ$ と近似できるので， $ω = \sqrt{g / L}$ とおくと，式(1)は

$\frac{d^{2} θ}{d t^{2}} \approx - \frac{g}{L} θ$ $= - ω^{2} θ$ ---- (2)

と書くことができ，この微分方程式の解は単振動

$θ (t) = θ_{0} \cos (ω t + α)$ ---- (3)

で表される．ここで，周期は

$T = \frac{2 π}{ω}$ $= 2 π \sqrt{\frac{L}{g}}$ ---- (4)

である．式(4)の両辺を2乗すると

$T^{2} = \frac{4 π}{g} L$

となり，単振り子の長さ $L$ と周期の2乗 $T^{2}$ との間には線形関係があることが分かる．

【参照】単振り子の近似解

【実験器具】

No.	品名	サイズなど	数量
1	ゴルフボール	約 43 mm	1個
2	ヒートン（吊り金具）	8-10 mm 程度	1個
3	糸（ナイロン・ポリエステルなど）	長さ 1 m 程度，Φ 0.6-0.8 mm 程度	1本
4	支持棒（アルミ丸パイプなど）	長さ 10 cm 程度，Φ 4 mm 程度	1本
5	ノギス	－	1個
6	ストップ付コンベックス	1 m 以上測れるもの	1個
7	ストップウォッチ	－	1個
8	ガムテープ	－	適量

※ サイズにおいて，Φ（ファイ）は直径を表す．

【実験の準備】

図のように，ゴルフボール（器具1）にヒートン（器具2）を取り付け，糸（器具3）を結びつける．ここでは，ゴルフボールを振り子のおもりとして使用するが，糸が結び付けられる吊り具の付いた比較的密度の高い小物体であればよい．

十分な高さのある机に振り子支持棒（器具4）をガムテープで水平に固定し，おもり（ゴルフボール）が床につかないように糸の長さを調節して，糸を支持棒に固定する．振り子の長さ $L$ は支持棒に固定した点からおもりの重心までの長さである（球の重心は球の中心である）．また，糸の質量は無視できるものとする．ゴルフボールの直径 $2 r$ をノギス（器具5）で測定し，糸の長さ $l$ をコンベックス（器具6）で測定して，振り子の長さ $L = r + l$ とする．

必要に応じて，振り子の背後に大きめの紙を貼り，振り子を静止させて，正面から見て振り子の糸と一致するように，紙面に直線（鉛直線）を引く．これは測定時にストップウォッチのボタンを押すタイミングの目安とするためである（振り子の糸が紙面に引いた直線に一致した瞬間にスタート・ストップする．）

【測定方法】

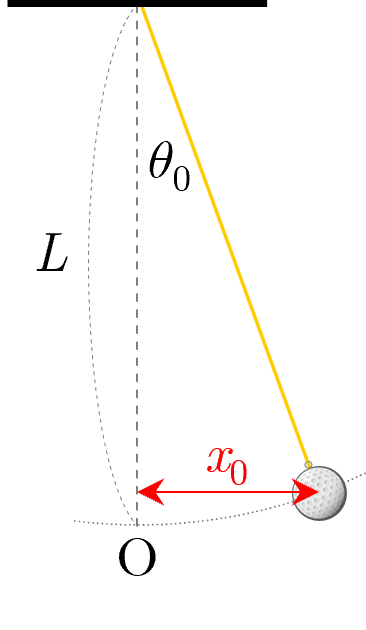
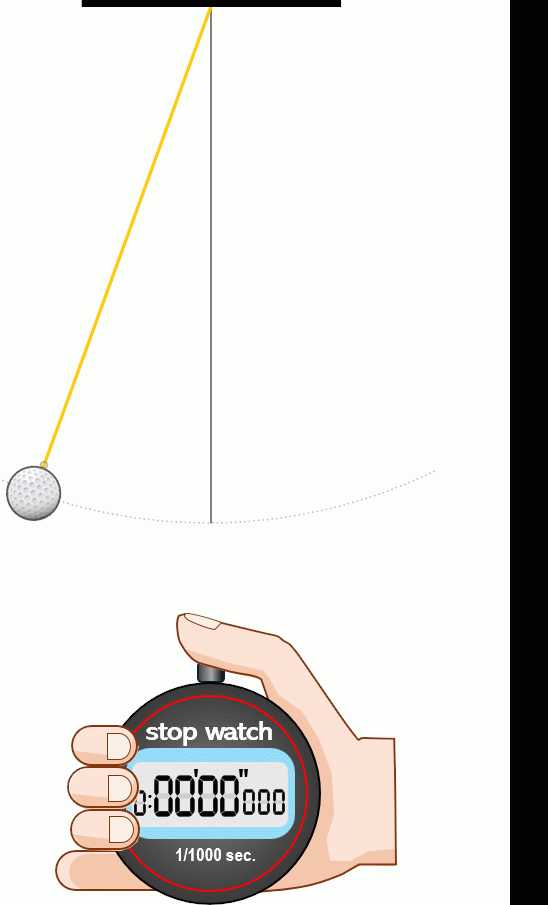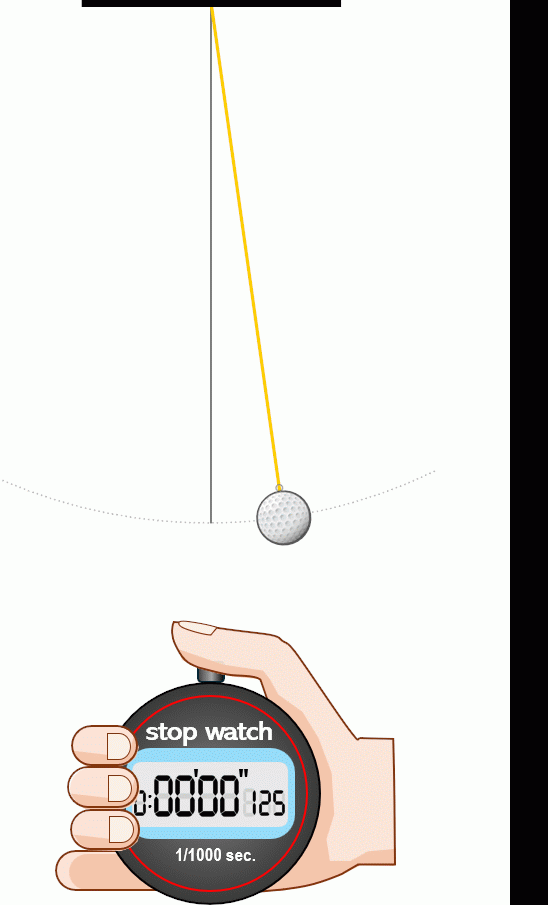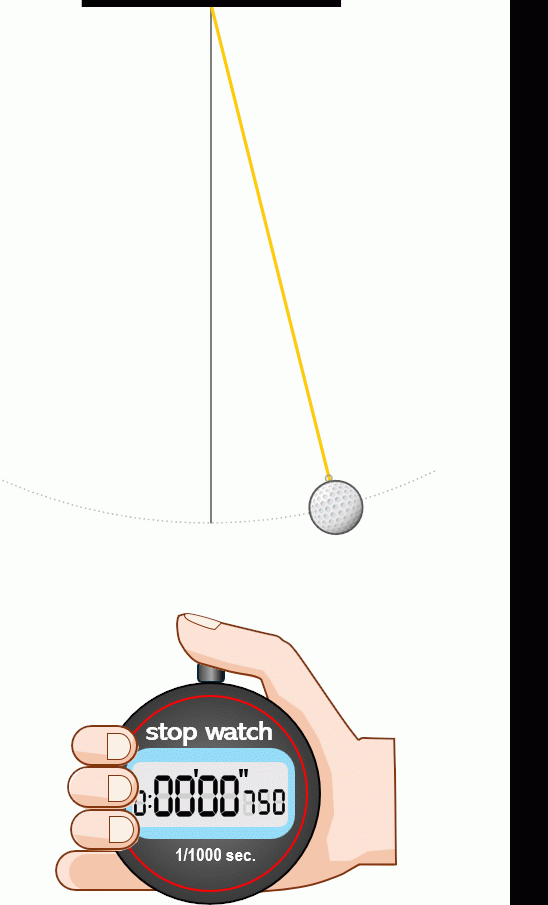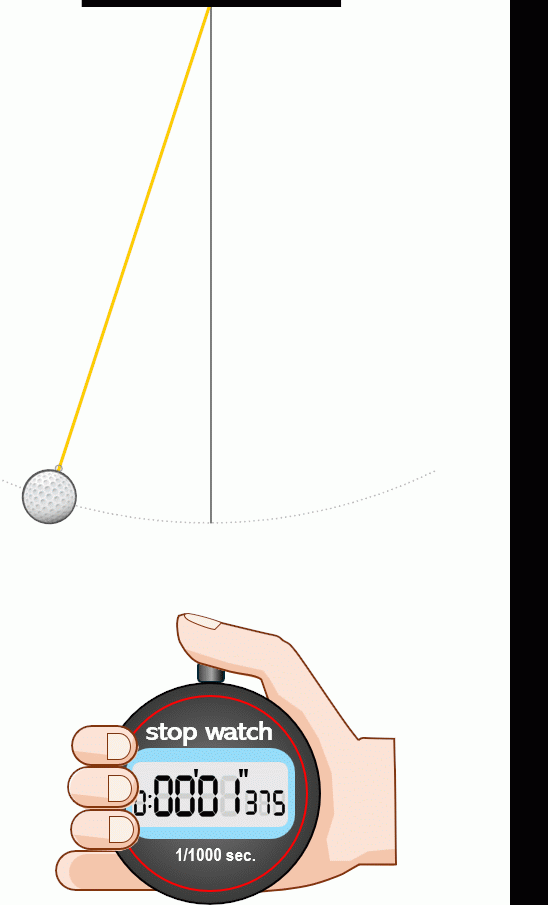
振り子が静止した状態から，おもりを距離 $x_{0}$ だけ引いて（ $x_{0}$ はできるだけ小さく），静かに振動を開始させる．このとき，振り子のおもりが鉛直面内で振動するように（楕円軌道を描いたりしないように）注意する．また，糸の捻じれによっておもりが自転しないように気を付ける．

振り子が5往復にかかる時間を計測する．この際，振り子の背後に鉛直線を引いておくと，振り子の糸が鉛直線と重なった瞬間にストップウォッチのスタート・ストップボタンを押せばよい（糸が鉛直線を同一方向に5回通過したときの時間を計測する）．1往復だけの時間を測定するのは誤差が大きくなるため，ここでは5往復にかかる時間を測定するとしているが，10往復などでも構わない．

振り子の長さ $L$ を変えて，同様の計測を行い，測定結果を集計する（下に示すような集計表に記入するとよい）．可能であれば，1つの振り子の長さに対して，5往復にかかる時間を複数回測定し，その平均を取るとよい．

【集計表】

測定結果をもとに，振り子の周期 $T$ ，周期の2乗 $T^{2}$ をそれぞれ計算し，有効数字を考慮して集計表に記入する．（下表では，ゴルフボールの半径 $r$ ，糸の長さ $l$ ，＃往復にかかる時間を入力して，集計ボタンを押せば，振り子の長さ $L$ ，周期 $T$ ，周期の2乗 $T^{2}$ を自動的に計算する．）

おもり（ゴルフボール）の半径 $r =$ 〔m〕

糸の長さ $l$ 〔m〕
振り子の長さ $L$ 〔m〕
往復にかかる時間〔s〕
振り子の周期 $T$ 〔s〕
周期の2乗 $T^{2}$ 〔s²〕

【解析】

測定したデータについて，グラフ用紙（標準方眼用紙）を用いて，横軸に周期の2乗 $T^{2}$ ，縦軸に振り子の長さ $L$ をとって散布図を描く（参考：グラフの作成の仕方）．上述の理論（単振り子の近似解）によると，振り子の長さ $L$ と周期の2乗 $T^{2}$ との間には

$L = \frac{g}{4 π} T^{2}$ ---- (5)

の線形関係がある．原点を通って，描いた散布図のデータを最もよく表す近似直線（回帰直線）を引き，その近似直線の傾きと式(5)との関係から，重力加速度の大きさ $g$ を見積もる．もちろん，グラフ作成にはExcelのようにグラフを作成できるソフトウェアを用いるのもよいであろう（Excelには回帰直線を自動で引いてくれる機能がある）．

振り子の長さ $L$ を，見積もられた $g$ の値の1/4の長さに調整して（ $L = g / 4$ ），振り子を微小振動させ周期 $T$ を測定すると近似的に $π$ の値を求めることができる：

$∵ T = 2 π \sqrt{\frac{L}{g}}$ $= 2 π \sqrt{\frac{g / 4}{g}}$ $= 2 π \cdot \frac{1}{2}$ $= π$

※ $g \approx 9.8$ ${m/s}^{2}$ より $9.8 / 4 = 2.45$ $m$ なので，十分高い天井などに支点を設ける必要があろう．

集計・解析が終われば，実験レポートを作成する（参考：実験レポートの書き方）．

ホーム>>カテゴリ>>物理実験モジュール>>単振り子実験モジュール>>簡易単振り子実験モジュール