角運動量 (angular momentum)

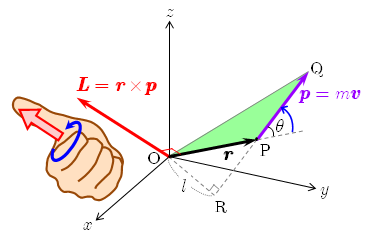
質量 ${\displaystyle m}$ の質点が速度 ${\displaystyle \mathit{v}}$ で運動している，つまり運動量 ${\displaystyle \mathit{p}=m\mathit{v}}$ で運動しているとき，その質点の位置ベクトルを ${\displaystyle \mathit{r}}$ とすると，ベクトル ${\displaystyle \mathit{p}}$ の点 O のまわりのモーメントは

${\displaystyle \mathit{L}=\mathit{r}\times \mathit{p}}$     - - - (1)

である(成分表示)．この運動量のモーメント ${\displaystyle \mathit{L}}$ を，質点が点 O のまわりにもつ 角運動量 (angular momentum) という．

角運動量は物体の回転運動において重要な概念であり，簡単にいえば回転運動の勢いを表す量である．

図のように，運動量 ${\displaystyle \mathit{p}}$ をもつ質点の位置を点 P とする．式(1)より，角運動量 ${\displaystyle \mathit{L}}$ は ${\displaystyle \mathit{r}}$ と ${\displaystyle \mathit{p}}$ のベクトル積（外積）で定義されるので， ${\displaystyle \mathit{L}}$ の方向は ${\displaystyle \mathit{r}}$ と ${\displaystyle \mathit{p}}$ で張られる平面（淡緑の面）に垂直で， ${\displaystyle \mathit{r}}$ と ${\displaystyle \mathit{p}}$ のなす角 ${\displaystyle \theta }$ について ${\displaystyle \mathit{r}}$ から ${\displaystyle \mathit{p}}$ に回転するときに右ネジが進む方向（図の右手の親指の方向）を向いている．また，位置ベクトルの大きさ ${\displaystyle r=\left|\mathit{r}\right|}$ ，運動量の大きさ ${\displaystyle p=\left|\mathit{p}\right|}$ を用いて， ${\displaystyle \mathit{L}}$ の大きさは

${\displaystyle L=\left|\mathit{L}\right|=rp\sin \theta }$     - - - (2)

と表される．点 O から PQ を通る直線に下ろした垂線の長さ ${\displaystyle l=\left|\mathit{r}\right|\sin \theta }$ より， ${\displaystyle L=lp}$ と書けて，これは形式的には図の △OPQ の面積の2倍に等しいといえる．

• 角運動量の成分表示
• 角運動量の向き
• 異なる座標原点
• 回転運動の法則
• 角運動量保存の法則

ホーム>>カテゴリー分類>>力学>>運動>>角運動量

[ページトップ]

利用規約

google translate (English version)