|
ローレンツ力 (Lorentz force)
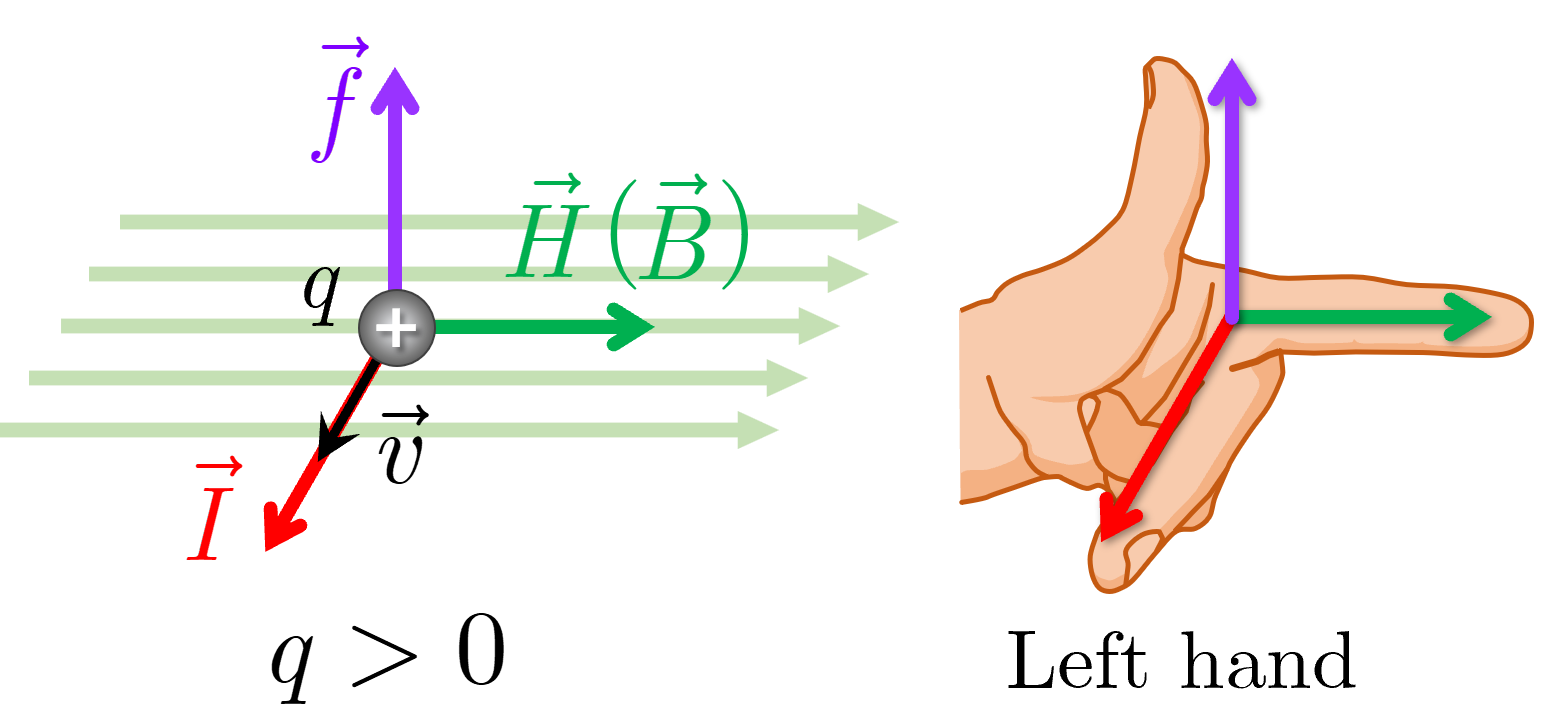
図1
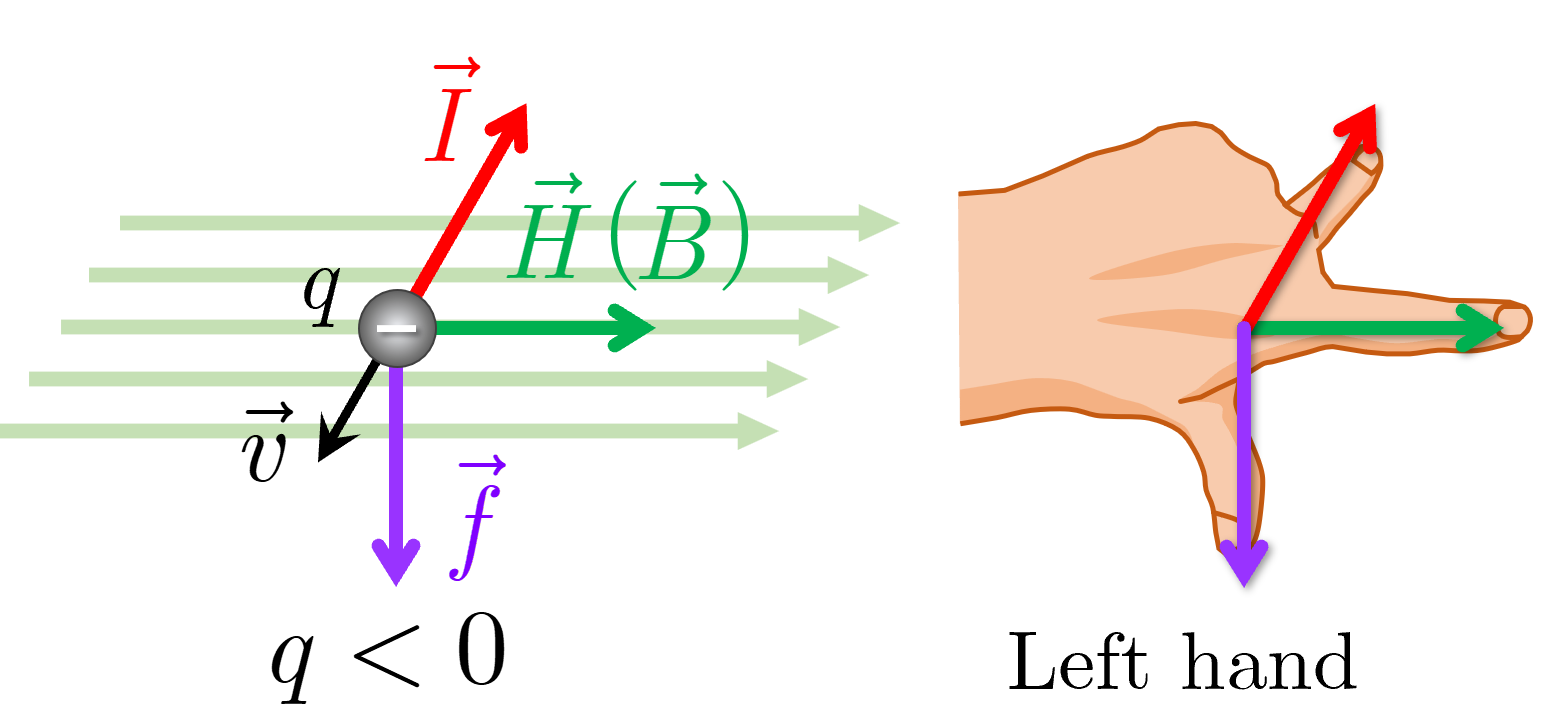
図2
電気を帯びた粒子(荷電粒子)が磁場中を運動するときに,荷電粒子が磁場から受ける力を ローレンツ力 (Lorentz force) という.大きさ の磁束密度の磁場中で,電気量 をもつ荷電粒子が磁場に垂直な向きに速さ で運動しているとき,この荷電粒子にはたらくローレンツ力の大きさは
となる.その力の向きは,正電荷( )の運動の向きを電流の向きと考えるとフレミングの左手の法則によって定まる(図1).負電荷( )の場合は,電流の向きを運動の向きと逆向きに考えてフレミングの左手の法則を適用すると,ローレンツ力の向きは正電荷の場合と反対向きとなる(図2).
このローレンツ力の大きさは,電流が磁場(磁界)から受ける力から導くことができる.大きさ の磁束密度の磁場中に,磁場と垂直に置かれた導線に大きさ の電流を流すと,導線の長さ の部分には大きさ
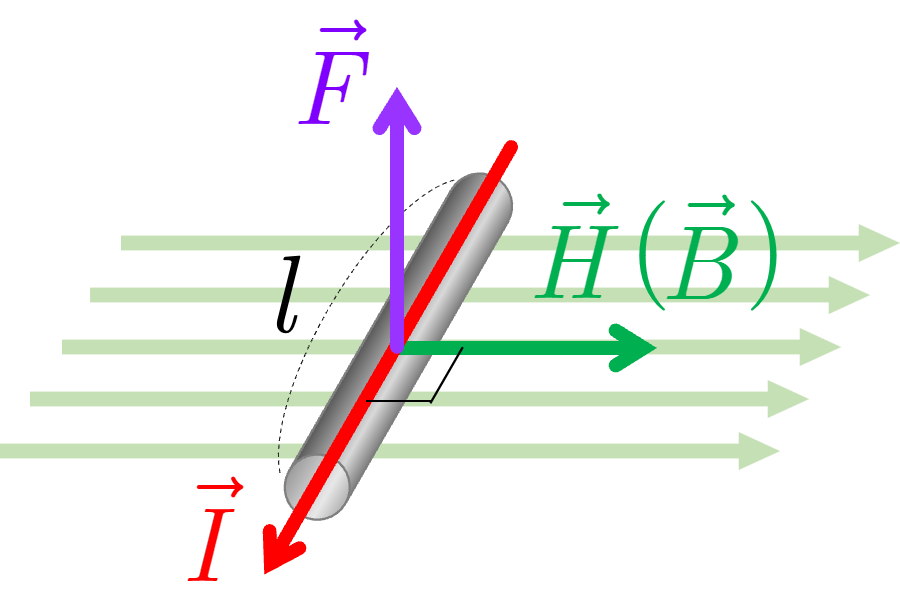
図3
の電磁力がはたらく(図3).この導線の断面積を ,導体 当たりの自由電子(電気量 )の数を ,自由電子の平均の速さを とすると,電流の定義より電流の大きさは
と表される.また,導線の長さ の部分に含まれる自由電子の数は, 個と表される.自由電子 個が受けるローレンツ力の大きさを とすると,導線 の受ける力の大きさ は,この中に含まれる 個の自由電子が受けるローレンツ力の合計であるので,
が得られる.
また,荷電粒子の速度の向きと磁場の向きが垂直ではなく角 をなす場合は,磁場と垂直な速度の成分 を用いてローレンツ力の大きさを と表す.
ホーム>>物理>>第4編 電気と磁気>>第3章 電流と磁場>>ローレンツ力
学生スタッフ作成
2024年2月22日