2次関数のグラフの式を求める問題

■問題

放物線 ${\displaystyle y=-2x^2+4x+7}$ と直線 ${\displaystyle y=2x-5}$ の交点を求めよ．

■解説動画

◆関連動画のページへ

■答

$\left(-2,-9\right)$ ， $\left(3,1\right)$

■解説

${\displaystyle y=-2x^2+4x+7}$ ･･････(1)

${\displaystyle y=2x-5}$ ･･････(2)

(1)と(2)のグラフの交点を求めることは，(1)と(2)に共通する $x$ と $y$ の組を求めることである．よって，(1)と(2)の連立方程式の解を解けばよい．

まず，(1)ー(2)の計算を行い $y$ を消去すると

$0=-2x^2+2x+12$ ･･････(3)

が得られる．

(3)の $x$ の2次方程式を解く．

$-2x^2+2x+12=0$

因数分解する

$-2\left(x^2-x-6\right)=0$

$-2\left(x+2\right)\left(x-3\right)=0$

よって

$x=-2,3$

となる．

(2)に $x=-2$ を代入すると

$y=2\left(-2\right)-5=-9$

(2)に $x=3$ を代入すると

$y=2\cdot 3-5=1$

となる．

以上より，求める交点は

$\left(-2,-9\right)$ ， $\left(3,1\right)$

である．

●グラフ

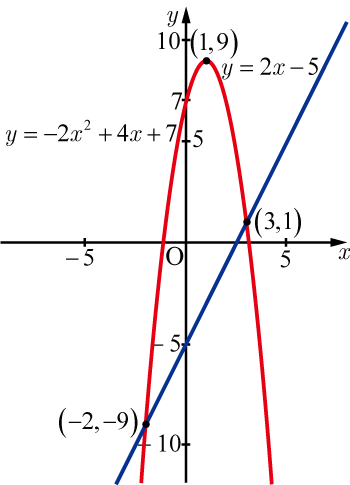
(1)を平方完成する

$y=-2x^2+4x+7$

$=-2\left(x^2-2x\right)+7$

$=-2{\left(x-1\right)}^2+9$

よって，放物線の頂点は

$\left(1,9\right)$

である．

 

ホーム>>カテゴリー分類>>関数>>関数の演習問題>>1次関数，2次関数などに関する問題>>直線の方程式に関する問題

最終更新日： 2025年4月18日