1次不等式に関する問題

■問題

1次不等式

${\displaystyle 4>3x-8}$ ･･････(1)

の解を求めよ．

■解説動画

◆関連動画のページへ

■答

$x<4$

■解説

(1)の両辺から $3x$ を減じる(不等式の性質2)ことにより，(1)の右辺の $3x$ を左辺に移項する．

$4-3x>3x-8-3x$ ･･････(2)

${\displaystyle 4-3x>-8}$

次に，(2)の両辺から $4$ を減じる(不等式の性質2)ことにより，(2)の左辺の $4$ を右辺に移項する．

${\displaystyle 4-3x-4>-8-4}$

${\displaystyle -3x>-8-4}$

移項できたので，右辺を簡単にする．

${\displaystyle -3x>-12}$ ･･････(3)

(3)の両辺を $-3$ で割る． $-3$ は負の値なので不等号の向きが変わる．（不等式の性質7）.

${\displaystyle \frac{-3x}{-3}<\frac{-12}{-3}}$ ･･････(4)

(4)の両辺を約分する．

${\displaystyle x<4}$

以上で解が求まった．

●別解

(1)の左辺と右辺を入れ換える．不等式なので不等号の向きも変える．

${\displaystyle 3x-8<4}$ ･･････(5)

(5)の両辺に $8$ を加える(不等式の性質1)ことにより，(5)の左辺の $8$ を右辺に移項する．

$3x-8+8<4+8$

$3x<4+8$

移項できたので，右辺を簡単にする．

$3x<12$ ･･････(6)

(6)の両辺を $3$ で割る． $3$ は正の値なので不等号の向きは変わらない．（不等式の性質4）.

${\displaystyle \frac{3x}{3}<\frac{12}{3}}$ ･･････(4)

(4)の両辺を約分する．

${\displaystyle x<4}$

以上で解が求まった．

●グラフによる確認

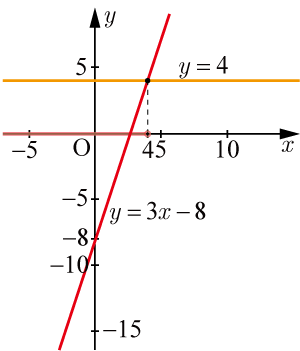
グラフより，(1)が成り立つのは

${\displaystyle x<4}$

であることが確認できる．

 

ホーム>>カテゴリー分類>>関数>>関数の演習問題>>方程式・不等式に関する問題>>1次不等式に関する問題

最終更新日： 2025年4月18日