置換積分の問題

■問題

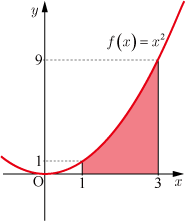
曲線 ${\displaystyle f\left(x\right)=x^2}$ と ${\displaystyle x}$ 軸と直線 ${\displaystyle x=1}$ ， ${\displaystyle x=3}$ で囲まれた面積を右端区分求積法より求めよ．

■解説動画

◇積分の動画一覧のページへ

■答

${\displaystyle \frac{26}{3}}$

■ヒント

区分求積法を参考にする．

■解説

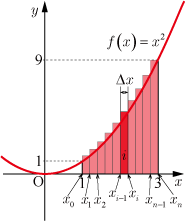
区間 ${\displaystyle \left[1,3\right]}$ を ${\displaystyle n}$ 等分する． ${\displaystyle x_0=1}$ ， ${\displaystyle x_n=3}$ とし，間の分点を ${\displaystyle x_1}$ ， ${\displaystyle x_2}$ ，･･･， ${\displaystyle x_{i-1}}$ ， ${\displaystyle x_i}$ ，･･･， ${\displaystyle x_{n-1}}$ とする．右端区分求積法を用いるので図のように求める面積を長方形の面積の和 ${\displaystyle S_n}$ で近似する．

$i$ 番目の長方形の面積 ${\displaystyle A_i}$ を求める．

$i$ 番目の長方形の幅： ${\displaystyle \Delta x=\frac{3-1}{n}=\frac{2}{n}}$ ･･････(1)

$i$ 番目の長方形の高さ： ${\displaystyle f\left(x_i\right)=f\left(1+\frac{2}{n}i\right)={\left(1+\frac{2}{n}i\right)}^2}$ ･･････(2)

よって

${\displaystyle A_i=f\left(x_i\right)\Delta x}$ ${\displaystyle ={\left(1+\frac{2}{n}i\right)}^2\frac{2}{n}}$ ･･････(3)

となる．

${\displaystyle n}$ 個の長方形の面積の和を ${\displaystyle S_n}$ とすると

${\displaystyle S_n={\displaystyle \sum }_{i=1}^n{A}_i={\displaystyle \sum }_{i=1}^n{\left(1+\frac{2}{n}i\right)}^2\frac{2}{n}}$ ･･････(4)

となる．

求める面積 ${\displaystyle S}$ は

${\displaystyle S=\underset{n\to \infty }{\lim }{S}_n}$ （このページの参考を参照）　･･････(5)

より

${\displaystyle S=\underset{n\to \infty }{\lim }{\displaystyle \sum }_{i=1}^n{\left(1+\frac{2}{n}i\right)}^2\frac{2}{n}}$ ･･････(6)

${\displaystyle =\underset{n\to \infty }{\lim }{\displaystyle \sum }_{i=1}^n\left(\frac{2}{n}+\frac{8}{n^2}i+\frac{8}{n^3}{i}^2\right)}$

${\displaystyle =\underset{n\to \infty }{\lim }\frac{2}{n}{\displaystyle \sum }_{i=1}^{n}1+\underset{n\to \infty }{\lim }\frac{8}{n^2}{\displaystyle \sum }_{i=1}^{n}i+\underset{n\to \infty }{\lim }\frac{8}{n^3}{\displaystyle \sum }_{i=1}^n{i}^2}$

この右端型の区分求積法を定積分の式で表すと

${\displaystyle \underset{n\to \infty }{\lim }{\displaystyle \sum }_{i=1}^n{\left(1+\frac{2}{n}i\right)}^2\frac{2}{n}={\displaystyle {\int }_1^3{x}^{2}dx}}$ ･･････(7)

となる．この定積分を計算すると

${\displaystyle {\displaystyle {\int }_1^3{x}^{2}dx}={\left[\frac{1}{3}{x}^3\right]}_1^3}$ ${\displaystyle =\frac{1}{3}\cdot 3^3-\frac{1}{3}\cdot 1^3}$ ${\displaystyle =\frac{26}{3}}$ ･･････(8)

となり，当然ながら，(6)の計算結果と一致している．

ホーム>>カテゴリー分類>>積分>>積分の問題>>定積分の問題>>区分求積法の問題

最終更新日： 2025年6月9日