ベクトルに関する問題
■問題
三角形 の各頂点 , , と各対辺の中点のを結ぶ3つの線分(中線)は1点で交わることを示せ.
■解説動画
◇ベクトルに関する動画一覧のページへ
■ヒント
線分 の中点を , の中点を , の中点を とすると, 3つの中線は 線分 , 線分 , 線分 である. 線分 と 線分 の交点を 点 , 線分 と 線分 の交点を 点 , 線分 と 線分 の交点を 点 とする. 証明は,点 ,点 ,点 が一致することを示せばよい.
■答
三角形 の角頂点 , , の位置ベクトルを , , とし.位置ベクトルの始点を点 とする.
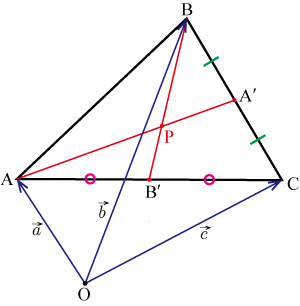
●点 を位置ベクトル , , で表す
点 は中線 上にあることより
( は定数)
| 点
は
線分
の中点,すなわち,
線分
を
に内分する点であるので
となる |
・・・・・・(1)
点 は中線 上でもあることより
( は定数)
| 点
は
線分
の中点,すなわち,
線分
を
に内分する点であるので
となる |
・・・・・・(2)
(1),(2)より
となる連立方程式が得られる.
(5)より
・・・・・・(6)
(6)を(3)に代入する.
・・・・・・(7)
(6)を(4)に代入する.
・・・・・・(8)
(7),(8)は(6)を満たしている.以上より連立方程式の解は
・・・・・・(9)
となる.
(9)を(1)に代入すると
・・・・・・(10)
●点 を位置ベクトル , , で表す
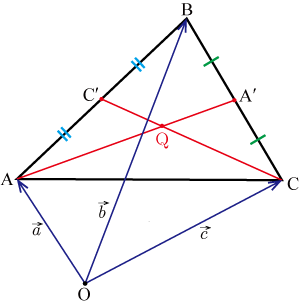
と同様にして を位置ベクトル , , を用いて表すと
・・・・・・(11)
となる.
●点 を位置ベクトル , , で表す
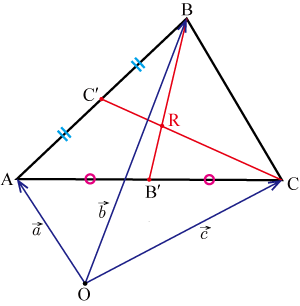
と同様にして を位置ベクトル , , を用いて表すと
・・・・・・(12)
となる.
●(10),(11),(12)より
となり,三角形 の各頂点 , , と各対辺の中点のを結ぶ3つの線分(中線)は1点で交わる.
この交点のことを重心といい,(9)の より
, ,
よって,重心は中線を に内分する.
ホーム>>カテゴリー分類>>ベクトル>>ベクトルに関する問題>>ベクトルに関する問題
最終更新日: 2026年1月21日