和の極限としての定積分の定義

原始関数で定積分を定義すると，定積分の意味することがらが理解しにくい．よって，和の極限としての定積分の定義を以下に示す．

関数 ${\displaystyle f\left(x\right)}$は閉区間 ${\displaystyle \left[a,b\right]}$ で定義されている． この区間${\displaystyle \left[a,b\right]}$を

${\displaystyle a=x_0<x_1<x_2<\cdots }$${\displaystyle <x_{n-1}<x_n=b}$

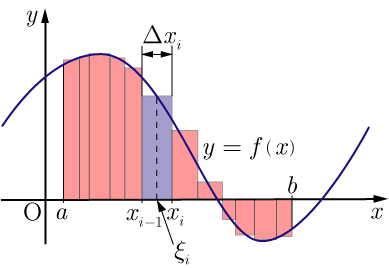
となる${\displaystyle x_i\left(i=0,1,2,\cdots ,n\right)}$でn 個の小区間に分割し， ${\displaystyle \Delta x_i=x_i-x_{i-1}}$　${\displaystyle \left(i=1,2,3,\cdots ,n\right)}$と定める． ${\displaystyle \Delta x_i}$の中で最大の値を ${\displaystyle \Delta }$ で表す．それぞれの区間 ${\displaystyle \left[x_{i-1},x_i\right]}$の中に任意の点${\displaystyle {\xi }_i}$をとり，${\displaystyle \Delta S_i=f\left({\xi }_i\right)\Delta x_i}$となる値を ${\displaystyle i=1}$からn まで足し合わせた値（リーマン和と呼ぶ）

${\displaystyle S_n=\sum _{i=1}^n\Delta S_i}$

${\displaystyle =\sum _{i=1}^{n}f\left({\xi }_i\right)\Delta x_i}$

${\displaystyle =\sum _{i=1}^{n}f\left({\xi }_i\right)\left(x_i-x_{i-1}\right)}$

を考える． ここで，閉区間${\displaystyle \left[a,b\right]}$の分割数n の値を大きくしていく（${\displaystyle \Delta }$の値を小さくしていく）と，分割の仕方および${\displaystyle {\xi }_i}$のとり方に関係なくある値S に収束するなら，式で示すと，

${\displaystyle S=\underset{n\to \infty }{lim}\sum _{i=1}^{n}f\left({\xi }_i\right)\left(x_i-x_{i-1}\right)}$

となるなら，${\displaystyle f\left(x\right)}$ は${\displaystyle \left[a,b\right]}$で積分可能であるといい，

${\displaystyle S={\int }_a^{b}f\left(x\right)dx}$

と表し，a からb までの定積分という．

閉区間 ${\displaystyle \left[a,b\right]}$ で関数${\displaystyle f\left(x\right)}$ が連続ならば， ${\displaystyle f\left(x\right)}$は ${\displaystyle \left[a,b\right]}$ で積分可能となる．

区間${\displaystyle \left[a,b\right]}$で${\displaystyle f\left(x\right)\geqq 0}$とすると，${\displaystyle \Delta S_i=f\left({\xi }_i\right)\Delta x_i}$の値は長方形の面積になり，分割を限りなく細かくしたときの長方形の面積の和，すなわち${\displaystyle {\int }_a^{b}f\left(x\right)dx}$は，関数${\displaystyle y=f\left(x\right)}$ の曲線とx 軸で挟まれた領域で，区間${\displaystyle \left[a,b\right]}$ の面積を表す（定積分と面積を参照のこと）．

 

ホーム>>カテゴリー分類>>積分 >>定積分の定義>>和の極限としての定積分の定義

最終更新日： 2023年7月3日