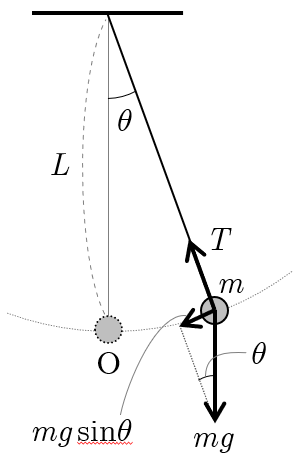
単振り子

運動方程式 ma=F に，加速度の接線方向成分 a=L d2θ dt2 と小球に作用する力の接線方向成分 F= −mgsinθ を代入すると，

         mL d2θ dt2 = −mgsinθ

を得る．

閉じる

sinθ≈θ を用いると， (1) の運動方程式は

         mL d2θ dt2 = −mgθ

となる．上式の両辺を mL で割って整理すると， θ についての定数係数の2階同次線形微分方程式

         d2θ dt2 +ω2θ =0   （ここで， ω= g/L とおいた．）

を得る（これは角振動数 ω の単振動の従う微分方程式である）．
上式の特性方程式は λ2+ ω2 =0 であるので，異なる2つの複素数解 λ=±iω をもつ．
よって，この微分方程式の一般解は

         θ(t)= c1cosωt +c2sinωt = c1 cosgLt +c2 singLt

と求まる．ここで c1 ,  c2 は任意定数である．また， A= c12 + c22 ， cosϕ= c1 /A ， sinϕ=− c2 /A とおいて，三角関数の合成を用いると，一般解は

         θ(t) =A c1A cosωt + c2A sinωt =A cosωtcosϕ − sinωtsinϕ
               =Acos ( ωt+ϕ ) = Acos gL t+ϕ

と表せる（単振動の解としては，こちらの表式が一般的である）．ここで c1 ,  c2 が任意定数なので， A, ϕ も任意定数である（ただし A>0 ）．

閉じる

角振動数 ω の単振動の周期 T= 2π/ω に ω= g/L を代入すると，

         T=2π Lg

を得る．上式より，周期は小球の質量に依存しないので，質量を4倍にしても周期は変化しない．糸の長さを4倍にすると，

         T′ =2π 4Lg = 2⋅2π Lg

となるので，周期は2倍になる．

閉じる