絶対値の記号を含む不等式の問題

■問題

次の不等式の解を求めよ．

$\left|2x+5\right|<x+7$ ･･････(1)

■答

$-4<x<2$

■ヒント

${\displaystyle 2x+5\geqq 0}$ の場合と ${\displaystyle 2x+5<0}$ に分けて考える．

■答

絶対値の性質1を用いて場合分けをする．

● ${\displaystyle 2x+5\geqq 0}$ ，すなわち， ${\displaystyle x\geqq -\frac{5}{2}}$ の場合

${\displaystyle \left|2x+5\right|=2x+5}$

より，(1)は

${\displaystyle 2x+5<x+7}$ ･･････(2)

となる．(2)を解くと

${\displaystyle x<2}$ ･･････(3)

となる．(2)の詳しい解き方は，この問題を参考にする．

(3)と ${\displaystyle x\geqq -\frac{5}{2}}$ の両方 を満たす範囲は

${\displaystyle -\frac{5}{2}\leqq x<2}$ ･･････(4)

となる．

● ${\displaystyle 2x+5<0}$ ，すなわち， ${\displaystyle x<-\frac{5}{2}}$ の場合

${\displaystyle \left|2x+5\right|=-\left(2x+5\right)}$

より，(1)は

${\displaystyle -\left(2x+5\right)<x+7}$ ･･････(5)

となる．(4)を解く．

${\displaystyle -2x-5<x+7}$

${\displaystyle -3x<12}$

$x>4$ ･･････(6)

となる．(6)と ${\displaystyle x<-\frac{5}{2}}$ の両方を満たす範囲は

${\displaystyle -4<x<-\frac{5}{2}}$ ･･････(7)

となる．

以上より

(1)の解は(4)と(7)を合わせた

$-4<x<2$

となる．

●グラフによる理解

$y=\left|2x+5\right|$ ･･････(8)

$y=x+7$ ･･････(9)

とおく．

以下に，(8)と(9)のグラフを示す．(1)の解は，(8)のグラフの(9)のグラフより下の部分の $x$ の範囲である

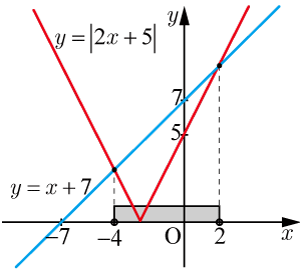
(8)のグラフのかき方はこのページを，(9)のページのグラフの書き方はこの問題を参考にしてください．

 

ホーム>>カテゴリー分類>>関数>>関数の演習問題>>方程式・不等式に関する問題>>絶対値の記号を含む不等式の問題

最終更新日： 2025年4月27日