不定積分の問題

■問題

次の問題を積分せよ（不定積分）．

${\displaystyle {\displaystyle \int \frac{1}{\sqrt{9-x^2}}dx}}$ 　　

■答

${\displaystyle {\sin }^{-1}\frac{x}{3}+C}$　　（$C$は積分定数）

■ヒント

基本となる関数の積分の「その他」よりこの

${\displaystyle {\displaystyle \int \frac{1}{\sqrt{a^2-x^2}}dx={sin}^{-1}\frac{x}{a}+C}}$　　（$C$は積分定数）

の公式を用いる．

■解説

${\displaystyle {\displaystyle \int \frac{1}{\sqrt{9-x^2}}dx}}$　･･････(1) 　

この問題では，公式の「${\displaystyle a^2}$」 は「${\displaystyle 9=3^2}$」 である．したがって

${\displaystyle ={\displaystyle \int \frac{1}{\sqrt{3^2-x^2}}dx}}$${\displaystyle ={\sin }^{-1}\frac{x}{3}+C}$　　（$C$は積分定数）

●別解1

${\displaystyle 9-x^2>0}$より，これを因数分解すると

${\displaystyle \left(3-x\right)\left(3+x\right)>0\\ }$

${\displaystyle \left(x-3\right)\left(x+3\right)<0}$

${\displaystyle -3<x<3}$

となる．よって

${\displaystyle x=3\sin \theta \left(-\frac{\pi }{2}<\theta <\frac{\pi }{2}\right)}$　･･････(2)

とおき，置換積分をする． ${\displaystyle \frac{dx}{d\theta }=3\cos \theta }$より

${\displaystyle dx=3\cos \theta d\theta }$　･･････(3)

となる．

(1)に(2)，(3)をそれぞれ代入し，置換積分すると

${\displaystyle {{\displaystyle \int }}^{\text{}}\frac{1}{\sqrt{9-x^2}}dx}$ ${\displaystyle ={{\displaystyle \int }}^{\text{}}\frac{3\cos \theta }{\sqrt{3^2\left(1-{\sin }^2\theta \right)}}d\theta }$

$={\displaystyle \int \frac{3\cos \theta }{\sqrt{3^2\left(1-{\sin }^2\theta \right)}}d\theta }$

$={\displaystyle \int \frac{3\cos \theta }{3\sqrt{1-{\sin }^2\theta }}d\theta }$

${\displaystyle {\sin }^2\theta +{\cos }^2\theta =1}$ → ${\displaystyle 1-{\sin }^2\theta ={\cos }^2\theta }$より

$={\displaystyle \int \frac{3\cos \theta }{3\sqrt{{\cos }^2\theta }}d\theta }$

${\displaystyle -\frac{\pi }{2}<\theta <\frac{\pi }{2}}$ → ${\displaystyle \cos \theta >0}$ → ${\displaystyle \sqrt{{\cos }^2\theta }=\cos \theta }$より

$={\displaystyle \int \frac{3\cos \theta }{3\cos \theta }d\theta }$

$={\displaystyle \int d\theta }$

${\displaystyle =\theta +C}$　･･････(4)

ここで，(2)を ${\displaystyle \theta =}$ の形に式を変形すると，（アークサイン参照）

${\displaystyle x=3sin\theta \to \theta ={sin}^{-1}\frac{x}{3}}$　･･････(5)

となる．(5)を(4)に代入すると

${\displaystyle \int \frac{1}{\sqrt{9-x^2}}dx={sin}^{-1}\frac{x}{3}+C}$　･･････(6)

となる．

●別解2

今回は

${\displaystyle x=3\cos \varphi \left(0<\theta <\pi \right)}$　･･････(7)

とおき，置換積分をする． ${\displaystyle \frac{dx}{d\theta }=-3\cos \varphi \theta }$より

${\displaystyle dx=-3\cos \varphi d\varphi }$　･･････(8)

となる．

(1)に(7)，(8)をそれぞれ代入し，置換積分すると

${\displaystyle {{\displaystyle \int }}^{\text{}}\frac{1}{\sqrt{9-x^2}}dx}$ ${\displaystyle ={{\displaystyle \int }}^{\text{}}\frac{-3\sin \varphi }{\sqrt{3^2\left(1-{\cos }^2\varphi \right)}}d\varphi }$

$={\displaystyle \int \frac{-3\sin \varphi }{\sqrt{3^2\left(1-{\cos }^2\varphi \right)}}d\varphi }$

$={\displaystyle \int \frac{-3\sin \varphi }{3\sqrt{1-{\cos }^2\varphi }}d\varphi }$

${\displaystyle {\sin }^2\varphi +{\cos }^2\varphi =1}$ → ${\displaystyle 1-{\cos }^2\varphi ={\sin }^2\varphi }$より

$={\displaystyle \int \frac{-3\sin \varphi }{3\sqrt{{\sin }^2\varphi }}d\varphi }$

${\displaystyle 0<\varphi <\pi }$ → ${\displaystyle \sin \varphi >0}$ → ${\displaystyle \sqrt{{\sin }^2\varphi }=\sin \varphi }$より

$={\displaystyle \int \frac{-3\sin \varphi }{3\sin \varphi }d\varphi }$

$={\displaystyle -\int d\varphi }$

${\displaystyle =-\varphi +C}$　･･････(9)

ここで，(7)を ${\displaystyle \varphi =}$ の形に式を変形すると，（アークコサイン参照）

${\displaystyle x=3cos\varphi \to \varphi ={cos}^{-1}\frac{x}{3}}$　･･････(10)

となる．(10)を(9)に代入すると

${\displaystyle \int \frac{1}{\sqrt{9-x^2}}dx=-{cos}^{-1}\frac{x}{3}+C}$　･･････(11)

となる．

(9)の $\varphi$ を(2)の $\theta$ に変換する．

下の図は， $x$ と $\varphi$ ， $\theta$ の関係を示す図である．

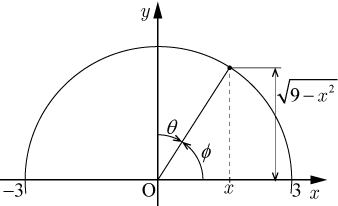
${\displaystyle x:-3\to 3}$ のとき，${\displaystyle \theta :-\frac{\pi }{2}\to \frac{\pi }{2}}$ ， ${\displaystyle \varphi :\pi \to -\pi }$ であることより， 図では角度 $\theta$の正方向は時計回り，角度 $\varphi$ の正方向は反時計回りとなる．よって， $\varphi$ と $\theta$ の関係は

${\displaystyle \theta +\varphi =\frac{\pi }{2}}$ 　→　 ${\displaystyle \varphi =\frac{\pi }{2}-\theta }$ 　･･････(12)

となる．(9)に(12)を代入すると

${\displaystyle \int \frac{1}{\sqrt{9-x^2}}dx}$ ${\displaystyle =-\left(\frac{\pi }{2}-\theta \right)+C}$ ${\displaystyle =\theta -\frac{\pi }{2}+C}$　･･････(13)

(13)に(5)を代入すると

${\displaystyle \int \frac{1}{\sqrt{9-x^2}}dx}$${\displaystyle ={\sin }^{-1}\frac{x}{3}-\frac{\pi }{2}+C}$　･･････(14)

(14)の ${\displaystyle -\frac{\pi }{2}+C}$ を改めて $C$ と書き換えると(6)になる．

【参考】

アークサインとアークコサインの関係

　

■確認問題

求まった答え ${\displaystyle {\sin }^{-1}\frac{x}{3}+C}$ を微分し，積分前の式 ${\displaystyle \frac{1}{\sqrt{9-x^2}}}$ に戻ることを確認しなさい．

　

ホーム>>カテゴリー分類>>積分>>積分の問題>>不定積分の問題>>${\displaystyle {\displaystyle \int \frac{1}{\sqrt{9-x^2}}dx}}$

最終更新日： 2024年8月2日