基本的な指数方程式の問題
■問題
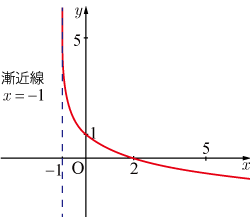
図は を漸近線とする対数関数のグラフである.グラフを表す関数の式を求めよ.
■解説動画
指数・対数の関連動画のページへ
■答
■ヒント
対数関数は一般的に
(対数関数の一般形) ・・・・・・(1)
と表せることを用いる.
グラフの漸近線は 軸である.
のグラフは, のグラフを 軸方向に , 軸方向に 平行移動したものになる.
したがって, のグラフの漸近線は, となる.
■解き方
漸近線が より
が得られ,(1)は
・・・・・・(2)
となる.
グラフが点 を通ることより
・・・・・・(3)
グラフが点 を通ることより
・・・・・・(4)
(3),(4)を連立させて, , を求める.
(3)より
・・・・・・(5)
が得られる.(5)を(4)に代入する.
(∵対数の定義)
(指数が負の場合を参照)
となる.
以上より,グラフを表す対数関数の式は
となる.底の変換公式を使って底を から に変更すると
となる.
ホーム>>カテゴリー分類>>指数/対数>>指数に関する問題>>基本的な指数方程式の問題
作成:学生スタッフ
最終更新日: 2025年4月18日