ラプラス変換に関する問題
■問題
次の式をラプラス変換を用いて,一般解を求めなさい.

(初期条件:=0%20%20}) ,
,=-%201%20%20}) )
)
■答

■ヒント
ラプラス変換の微分則を用いて解く
■解き方
ラプラス変換すると
})
-%20y%5cleft({0}%5cright)})
-%20s%5ccdot%20y%5cleft({0}%5cright)-%20{y}^{%5cprime%20}%5cleft({0}%5cright)})
となり,これらを式に代入
-%20sy%5cleft({0}%5cright)-%20{y}^{%5cprime%20}%5cleft({0}%5cright)%20%20})
-%20y%5cleft({0}%5cright)%20%20%5c)%20%20%20%20})
%20%20})

初期条件より
+1-%205%20sY%5cleft({s}%5cright)%20%20+4Y%5cleft({s}%5cright)=0})
%20%20Y%5cleft({s}%5cright)+1=0})
=-%20%5cfrac{%5chspace{2}1%5chspace{2}}{%5chspace{2}%20%20%5c(%20s-%201%20%20%5c)%20%20%20%5c(%20s-%204%20%20%5c)%20%20%20%20%5chspace{2}}})
ここで,部分分数分解をする.
=%5cfrac{%5chspace{2}%20%5chspace{1}{k}_{1}%20%20%5chspace{2}}{%5chspace{2}%20%20%5c(%20s-%201%20%20%5c)%20%20%20%20%5chspace{2}}+%5cfrac{%5chspace{2}%20%5chspace{1}{k}_{2}%20%20%5chspace{2}}{%5chspace{2}%20%20%5c(%20s-%204%20%20%5c)%20%20%20%20%5chspace{2}}})
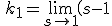%20%20%20%5c{%20-%20%5cfrac{%5chspace{2}1%5chspace{2}}{%5chspace{2}%20%20%5c(%20s-%201%20%20%5c)%20%20%20%5c(%20s-%204%20%20%5c)%20%20%20%20%5chspace{2}}%20%20%5c}%20%20%20%20})

%20%20%20%5c{%20-%20%5cfrac{%5chspace{2}1%5chspace{2}}{%5chspace{2}%20%20%5c(%20s-%201%20%20%5c)%20%20%20%5c(%20s-%204%20%20%5c)%20%20%20%20%5chspace{2}}%20%20%5c}%20%20%20%20})

よって
=%5cfrac{%5chspace{2}1%5chspace{2}}{%5chspace{2}3%5chspace{2}}%5ccdot%20%5cfrac{%5chspace{2}1%5chspace{2}}{%5chspace{2}%20%20%5c(%20s-%201%20%20%5c)%20%20%20%20%5chspace{2}}-%20%5cfrac{%5chspace{2}1%5chspace{2}}{%5chspace{2}3%5chspace{2}}%5ccdot%20%5cfrac{%5chspace{2}1%5chspace{2}}{%5chspace{2}%20%20%5c(%20s-%204%20%20%5c)%20%20%20%20%5chspace{2}}})
逆ラプラス変換をする ⇒ラプラス変換表はこちら

■別解
定数係数線形同次微分方程式の解法を用いて解く.
特性方程式

より
%20%20%20%5c(%20{%5clambda}-%204%20%20%5c)=0%20%20%20%20})

よって一般解は
 (ただし
(ただし は任意定数)
は任意定数)

初期条件より
=%5chspace{1}{C}_{1}+%5chspace{1}{C}_{2}}) ・・・・・・(1)
・・・・・・(1)
=%5chspace{1}{C}_{1}+4%5chspace{1}{C}_{2}}) ・・・・・・(2)
・・・・・・(2)
(1),(2)より

よって

ホーム>>カテゴリー分類>>微分>>ラプラス変換>>問題演習>>ラプラス変換に関する問題
最終更新日:
2023年6月6日