|
|||||||||||||
|
|||||||||||||
|
座標空間
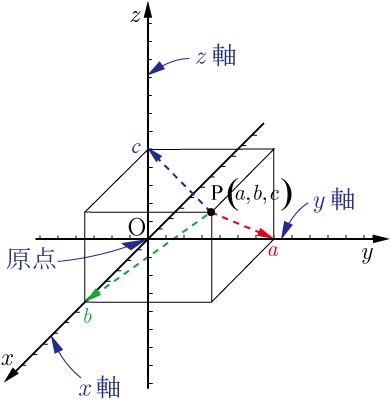 平面上に原点Oと,Oで互いに垂直に交わる直線を3つ定める.
平面上に原点Oと,Oで互いに垂直に交わる直線を3つ定める.
1つ目の直線上の点を原点Oからの距離に応じて変数 の値に対応させる.その直線を軸という.
2つ目の直線上の点を原点Oからの距離に応じて変数 の値に対応させる.その直線を軸という.
3つ目の直線上の点を原点Oからの距離に応じて変数 の値に対応させる.その直線を 軸という.
直線は原点Oによって,2つの半直線に分けられ,片方の半直線上の点を正の値に対応させ,他方の半直線上の点を負の値に対応させる.
, , に対応させる点を, 軸と 軸を含む平面( 平面)に平行で 軸上の に対応する点を通る平面と, 軸と 軸を含む平面( 平面)に平行で 軸上の に対応する点を通る平面と, 軸と 軸を含む平面( 平面)に平行で 軸上の に対応する点を通る平面との交点とする.すると , , の値の組に対応した点を空間上に定めることができる.
この空間のことを座標空間という.あるいは をつけて 座標空間という.
, , に対応させる点Pを という記号をもちいて表し, のことを点Pの座標という.点PをP ,点 ,座標 と表すこともある. また, を座標 の座標,(あるいは;成分),を座標 の座標,(あるいは 成分), を座標 の 座標,(あるいは 成分)という.
最終更新日: 2023年4月19日