回転行列 (rotation matrix)

原点を通る軸の周りの回転操作による座標変換は1次変換であり，その回転変換の表現行列を回転行列 (rotation matrix)という．ある軸 ${\displaystyle a}$ の周りに ${\displaystyle \theta }$ だけ回転（反時計回りを正とする）するときの回転行列 ${\displaystyle R_a(\theta )}$ は，

1.   ${\displaystyle R_a^{-1}(\theta )=R_a(-\theta )={}^{t}R{}_a(\theta )}$
2.   ${\displaystyle \det R_a(\theta )=1}$
3.   ${\displaystyle R_c(\phi )=R_b(\varphi )R_a(\theta )}$

という性質をもつ．性質 1, 2 より，回転行列は行列式が1の直交行列である．性質 3 は，軸 ${\displaystyle a}$ の周りに ${\displaystyle \theta }$ だけ回転してから軸 ${\displaystyle b}$ の周りに ${\displaystyle \varphi }$ だけ回転する操作は，ある軸 ${\displaystyle c}$ の周りに，ある角度 ${\displaystyle \phi }$ だけ回転することに等しい，ということを意味する（回転行列の積は回転行列）．

---

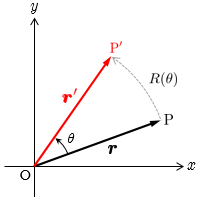
◆ 2次元の回転行列

${\displaystyle R(\theta )=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)}$       ⇒ 導出

${\displaystyle r^{\prime }=R(\theta )r}$ ${\displaystyle =\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)}$

${\displaystyle =\left(\begin{array}{c}x\cos \theta -y\sin \theta \\ x\sin \theta +y\cos \theta \end{array}\right)}$

平面座標の回転軸は ${\displaystyle xy}$ 面に垂直な軸のみなので， ${\displaystyle R}$ の添え字を省略する．回転軸が決まっているので平面座標の回転行列の積は次式を満たす．

${\displaystyle R(\theta )R(\varphi )=R(\varphi )R(\theta )=R(\theta +\varphi )}$

---

◆ 3次元の回転行列

■   ${\displaystyle x}$ 軸周り： ${\displaystyle R_x(\theta )=\left(\begin{array}{ccc}1& 0& 0\\ 0& \cos \theta & -\sin \theta \\ 0& \sin \theta & \cos \theta \end{array}\right)}$       ⇒ 導出

■   ${\displaystyle y}$ 軸周り： ${\displaystyle R_y(\theta )=\left(\begin{array}{ccc}\cos \theta & 0& \sin \theta \\ 0& 1& 0\\ -\sin \theta & 0& \cos \theta \end{array}\right)}$       ⇒ 導出

■   ${\displaystyle z}$ 軸周り： ${\displaystyle R_z(\theta )=\left(\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right)}$       ⇒ 導出

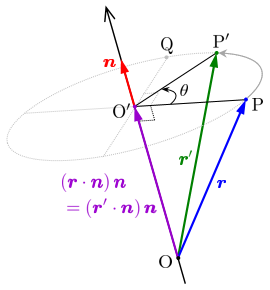
■  任意の軸周り（軸方向の単位ベクトルを ${\displaystyle n=(n_1,n_2,n_3)}$ とする）：

⇒ ロドリゲスの回転公式

ホーム>>カテゴリー分類>>行列>>線形代数>>回転行列

最終更新日：2023年1月14日