分布関数
確率変数
の任意の値とそのに対して
となる関数のことを分布関数あるいは累積分布関数という.(
の表現については,ここを参照)
分布関数
を確率関数
を用いて表現すると以下のようになる.
- 離散型確率変数の場合 ⇒
- 連続型確率変数の場合 ⇒
■事例
●事例1
サイコロを振った時の各目のでる確率に関する分布関数を描いてみる.確率変数
はサイコロの目の数とする.この場合の確率関数はここを参照する.
の場合:
の場合:
の場合:
の場合:
の場合:
の場合:
の場合:
よって,分布関数は以下の図のようになる.
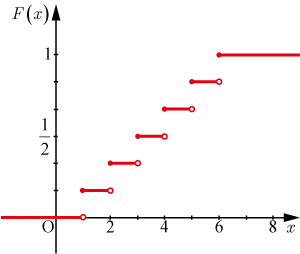
●事例2
標準正規分布の確率密度関数は
なので,累積分布関数は
ただし,
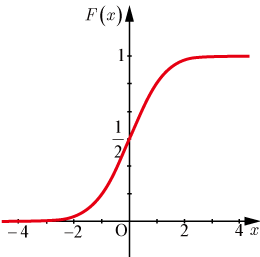
この関数のグラフは以下の図のようになる.
ホーム>>カテゴリー分類>>確率>>確率統計>>分布関数
最終更新日:
2024年2月1日

