中心極限定理のExcel教材1

■ダウンロード

中心極限定理Excel教材1⇒ダウンロード

【注意】教材のマクロを実行できるようにするためには，マクロのブロックを解除する必要があります。ここを参考にしてください。

■教材説明

Excel教材で確認する中心極限定理の性質

確率変数

$\bar{X} = \frac{1}{n} (X_{1} + X_{2} + \cdot \cdot \cdot + X_{n})$ 　･･････(1)

について

$E (\bar{X}) = μ$ 　･･････(2)

$V (\bar{X}) = \frac{σ^{2}}{n}$ 　･･････(3)

が成り立ち

「 $n \to + \infty$ のとき． $\bar{X}$ は，正規分布 $N (μ, \frac{σ^{2}}{n})$ に従う」　･･････(4)

が成り立つことを，5種類の確率密度関数(一様分布，右肩上がりの三角形状の分布，M字型の分布，右肩下がりの三角計上の分布，正規分布)を用いて，乱数を使って標本を無作為に取り出す操作をを繰り返し，得られたデータが上記性質を満たしているか確認をする．

Excel教材の概観を図1に示す．

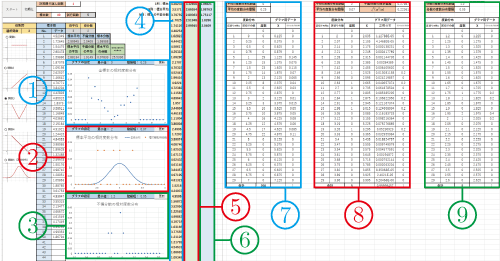
図1　Excel教材の概観

図2を用いてこの教材の使い方を説明する．

シミュレーションに用いる母集団を選択するために1番から5番のオプションボタンの中から1つをクリックする．オプションボタンの横に対応する確率密度関数のグラフが示されている．1番は一様分布，5番は正規分布になる．6番のセルに選択した確率分布の母平均と母分散が表示される．
7番のセルに母集団から無作為に取り出す標本数を入力する．
8番のセルに連続して標本を取り出す試行回数を設定する．
スタートボタンを押す．9番のセルに乱数関数のRAND()を用いたマクロにより母集団の中から指定した標本数のデータ(標本)が取り出される．10番のセルに取り出したデータ(標本)の平均，不偏分散，標本の分散が表示される．
12番のセルに試行回数が示されている．図2は5回標本を取り出す操作をした結果で，11番のセルに5回分の標本平均と標本分散から計算した値が計算されている．左から，標本平均の平均，不偏分散の平均，標本平均の分散，母分散と標本平均の分散の比(母分散/標本平均の分散)，である．
以上の操作で得られたデータを基にして，図1の1番，2番，3番のグラフが得られる．
再度，スタートボタンを押すと試行回数が累積される．

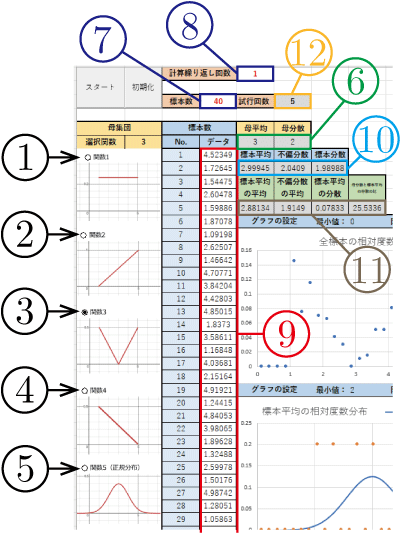
図2　図1の左上拡大

図3を用いて図1の3つのグラフの説明をする．図3では10000回標本を取り出す試行を実施した後に作成されたグラフである．

1番のグラフの青色の丸は，標本数40×試行回数10000回＝400000個の全標本を図1の7番の表で度数分布を計算し，その度数分布を相対度数分布に変換し，更に階級幅で割った値(確率密度に相当)を階級値のところにプロットしたものである．関数3の確率密度分布関数を持つ母集団から取り出した標本の分布になるので、その母集団の密度関数が再現されたグラフになっている．

2番のグラフのだいだいいろ色の丸は，各試行で得られた標本平均10000個分を図1の8番の表で度数分布を計算し，その度数分布を相対度数分布に変換し，更に階級幅で割った値(確率密度に相当)を階級値のところにプロットしたものである．実線は，中心極限定理から求められる正規分布のグラフである．だいだい色の丸が正規分布のグラフにほぼ重なるように分布しており，中心極限定理に従っていることが確認できる．

3番のグラフのだいだいいろ色の丸は，各試行で得られた標本分散10000個分を図1の8番の表で度数分布を計算し，その度数分布を相対度数分布に変換し，更に階級幅で割った値(確率密度に相当)を階級値のところにプロットしたものである．

標本数を変更すると分布が変化するので，初期設定の状態ではグラフがうまく表示されない場合がある．そのようば場合はグラフ上部の度数分布作成の設定値(階級の最小値，階級幅)を変更したり，Excelのグラフの調整機能を使って横軸の目盛りの設定などを変更してください．

初期化のボタンを押すと，図1中央部の灰色の列のデータ(4番，5番，6番のセルの値)と図2の12番の試行回数，10番の標本平均，不偏分散，標本分布，9番の標本数のデータの値，選択関数の選択が消去される．

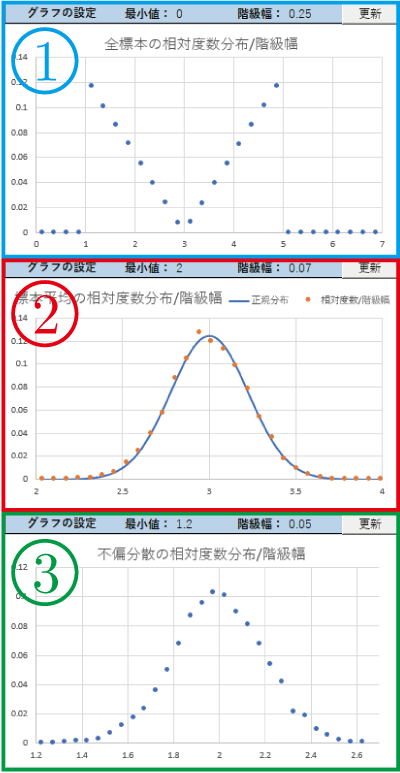
図3　累積サンプリング回数10000回後のグラフ

ホーム>>カテゴリー分類>>確率分布>>中心極限定理>>Excel教材

最終更新日： 2024年5月31日