F分布のExcel教材

■ダウンロード

$F$ 分布Excel教材⇒ダウンロード

【注意】教材のマクロを実行できるようにするためには，マクロのブロックを解除する必要があります。ここを参考にしてください。

■使い方

n1の値はχ12分布の自由度．1から8の間で変更可能．
n2の値はχ22分布の自由度．1から8の間で変更可能．
試行のボタンをクリックすると，D23セルでF分布に従う確率変数の値xを計算し，I列に追加する．
試行の繰り返し数：試行ボタンをクリックしたときの試行の繰り返し回数
H1セルの値は試行回数
初期化のボタンをクリックすると，H1セルの値を0にし、I列のデータを削除する．
計算値は，F分布の密度関数から計算をしている．
実験値は，I列のデータの度数分布(区間間隔0.1)から求めている．

■教材説明

$F$ 分布の性質

確率変数 $X$ ， $Y$ が互いに独立で，それぞれ自由度 $n_{1}$ ， $n_{2}$ の $χ^{2}$ 分布に従っているとき

$F = \frac{\frac{X}{n_{1}}}{\frac{Y}{n_{2}}}$ 　･･････(1)

は自由度 $(n_{1}, n_{2})$ のF分布に従う．

を用いて確率変数 $F$ の実現値を算出し，この実現値の分布が $F$ 分布になっているかどうかを確認する． $F$ 分布になっているかどうかの確認は，確率変数の実現値を数多く計算し、その度数分布とる．得られた度数分布から相対度数分布を計算し，その値を階級幅で割った値(確率密度に相当する)と $F$ 分布の確率密度関数のグラフを対応させることで行う．

Excel教材の概観を図1に示す．

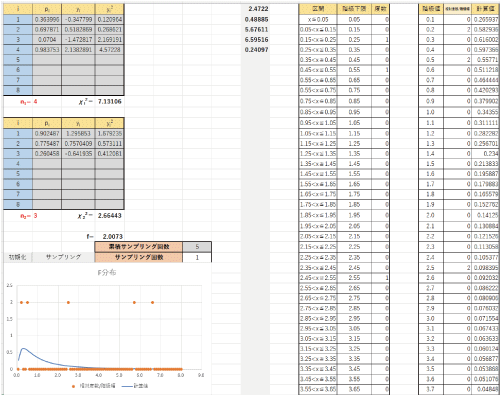
図1　Excel教材の概観

図2の1番，2番，3番のセルは，設定値を入力するためのセルである．

1番のセルは(1)の分子の $χ^{2}$ 分布の自由度 $n_{1}$ を設定する．初期値は4である．

2番のセルは(1)の分母の $χ^{2}$ 分布の自由度 $n_{2}$ を設定する．初期値は3である．

3番のセルは，連続してサンプリングする回数である．

以下に確率変数の実現値を算出する手順を示す．(自由度ｎ=4の場合)

4番の4つのセルにExcel関数のRAND()を用いて0から1の間の乱数を計算する．この値は確率密度関数の確率p_i(i=1,2,3,4)に相当する．
Excel関数のNORM.INV(累積確率,平均，標準偏差)を用いて，累積確率p_iに対応する標準正規分布の確率変数の実現値y_i(i=1,2,3,4)を算出する．（5番の4つのセル）
y_iの2乗y_i²を計算する．（6番の4つのセル）
y₁²+y₂²+y₃²+y₄²の値χ²を計算する．（7番のセルの値）このxの値が上記分子の $χ^{2}$ 分布の確率変数 $X$ の実現値χ²になる．
8番の4つのセルにExcel関数のRAND()を用いて0から1の間の乱数を計算する．この値は確率密度関数の確率p_i(i=1,2,3)に相当する．
Excel関数のNORM.INV(累積確率,平均，標準偏差)を用いて，累積確率p_iに対応する標準正規分布の確率変数の実現値y_i(i=1,2,3)を算出する．（9番の4つのセル）
y_iの2乗y_i²を計算する．（10番の4つのセル）
y₁²+y₂²+y₃²の値χ²を計算する．（11番のセルの値）このxの値が上記分母の $χ^{2}$ 分布の確率変数 $Y$ の実現値χ²になる．
12番のセルでは，確率変数 $F$ を計算する式(1)を用いて，上記の値からその実現値fを計算している．

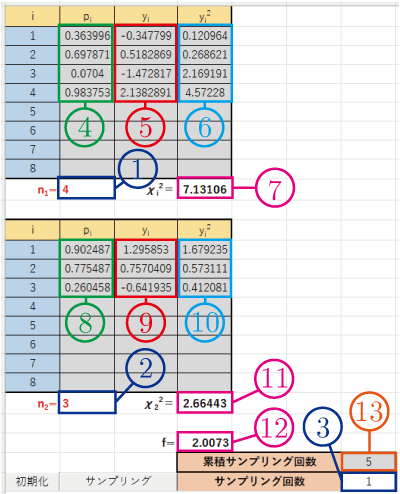
図2　図1の左上拡大

サンプリングのボタンを押すとマクロが実行され，fの値が図1中央部の灰色の列に上から順に入力される．図1はサンプリングを5回実行した結果である．サンプリングの実行回数(累積サンプリング回数)は図2の13番のセルに表示される．

3番のセルのサンプリング回数を，例えば100に変更してサンプリングのボタンを押すと一気に100回サンプリングが実行される．

図1の右から2つ目の表は，中央部の灰色の列に入力された確率変数の実現値から度数分布をExcel関数のFREQUENCYを用いて作成したものである．

図1の右端の表は，上記度数分布の表の度数から相対度数を計算し階級幅(区間幅の)で割った値(確率密度に相当する)変換したものと確率密度関数から階級値の確率密度を計算したものである．
【注意】相対度数を階級幅(区間の幅)で割った値は，階級幅が1より小さい場合は1を超える場合がある．確率密度に相当する値が1を超えるのはおかしいと思うかもしれないが，この教材の場合は階級幅が0.1であるので，相対度数が0.2なら相対度数を階級幅(区間の幅)で割った値は2になる．累積サンプリング回数が図1のように5回と少ない場合はこのようなことが生じる．

図1の左下のグラフは上記の相対度数を計算し階級幅(区間幅)で割った値の分布と確率密度関数の値から作成したグラフである．だいだい色の丸印は階級値に相対度数を階級幅(区間の幅)で割った値をプロットしたもので，実線は階級値における確率密度関数の値を曲線で結んだものである．

初期化のボタンを押すと，図1中央部の灰色の列のデータと累積サンプリング回数のデータが消去される．

図3は累積サンプリング回数10000回後のグラフである．だいだい色の丸印がが確率密度関数の実線上あるいはその近傍にあり，確率変数 $F$ が $F$ 分布に従っていることが確認できる．

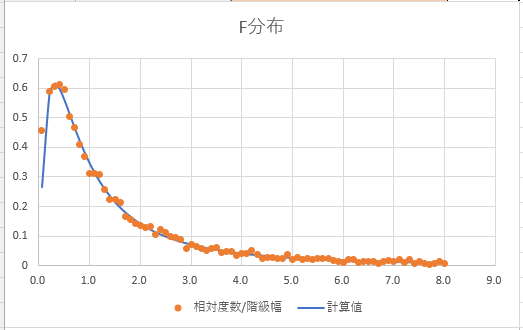
図3　累積サンプリング回数10000回後のグラフ

ホーム>>カテゴリー分類>>確率分布>>t分布>>Excel教材

最終更新日： 2024年5月29日