関連するページを見るにはこのグラフ図を利用してください．

離散型確率分布

離散型確率変数 ${\displaystyle X}$ について

${\displaystyle f\left(x_i\right)=P\left(X=x_i\right)}$     ${\displaystyle \left(i=1,2,\cdot \cdot \cdot ,n\right)}$

により定まる関数 ${\displaystyle f\left(x\right)}$ を確率変数 ${\displaystyle X}$ の確率関数（あるいは確率分布）という

■定理

${\displaystyle x_1,\cdot \cdot \cdot ,x_n}$ の値をとる離散型確率変数 ${\displaystyle X}$ の確率関数を ${\displaystyle f\left(x\right)}$ とするとき，以下の式が成り立つ．

• ${\displaystyle f\left(x_i\right)\geqq 0}$ ${\displaystyle \left(i=1,2,\cdot \cdot \cdot ,n\right)}$

  確率は $0$ 以上の値になるので，上式が成り立つ．

• ${\displaystyle \sum _{i=1}^{n}f\left(x_i\right)=1}$

  各確率変数 $X$ に対する確率の総和は $1$ になる．

• ${\displaystyle P\left(a\leqq X\leqq b\right)=\sum _{a\leqq x_i\leqq b}f\left(x_i\right)}$

■事例

●事例1

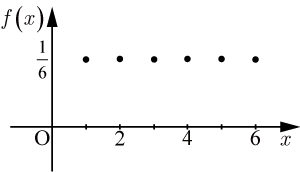
サイコロを振った時の各目のでる確率を以下に示す．確率変数 $X$ はサイコロの目の数とする．

${\displaystyle f\left(1\right)=P\left(X=1\right)=\frac{1}{6}}$ ， ${\displaystyle f\left(2\right)=P\left(X=2\right)=\frac{1}{6}}$ ， ${\displaystyle f\left(3\right)=P\left(X=3\right)=\frac{1}{6}}$ ， ${\displaystyle f\left(4\right)=P\left(X=4\right)=\frac{1}{6}}$ ， ${\displaystyle f\left(5\right)=P\left(X=5\right)=\frac{1}{6}}$ ， ${\displaystyle f\left(6\right)=P\left(X=6\right)=\frac{1}{6}}$

${\displaystyle =\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}}$ ${\displaystyle =1}$

${\displaystyle P\left(1\leqq X\leqq 3\right)}$ ${\displaystyle ={\displaystyle \sum _{1\leqq i\leqq 3}f\left(i\right)}}$ ${\displaystyle =f\left(1\right)+f\left(2\right)+f\left(3\right)}$ ${\displaystyle =\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=\frac{1}{2}}$

●事例2

2つのサイコロを振った時の出た目の和を確率変数 $X$ とする．

確率変数 $X$ は

$X=2,3,4,5,6,7,8,9,10,11,12$

となる.各確率変数 $X$ の値の場合の数(サイコロのでた目の組)を書き出すと

$X=2$ のとき： $\left(1,1\right)$

$X=3$ のとき： $\left(1,2\right)$ $\left(2,1\right)$

$X=4$ のとき： $\left(1,3\right)$ $\left(2,2\right)$ $\left(3,1\right)$

$X=5$ のとき： $\left(1,4\right)$ $\left(2,3\right)$ $\left(3,2\right)$ $\left(4,1\right)$

$X=6$ のとき： $\left(1,5\right)$ $\left(2,4\right)$ $\left(3,3\right)$ $\left(4,2\right)$ $\left(5,1\right)$

$X=7$ のとき： $\left(1,6\right)$ $\left(2,5\right)$ $\left(3,4\right)$ $\left(4,3\right)$ $\left(5,2\right)$ $\left(6,1\right)$

$X=8$ のとき： $\left(2,6\right)$ $\left(3,5\right)$ $\left(4,4\right)$ $\left(5,3\right)$ $\left(6,2\right)$

$X=9$ のとき： $\left(3,6\right)$ $\left(4,5\right)$ $\left(5,4\right)$ $\left(6,3\right)$

$X=10$ のとき： $\left(4,6\right)$ $\left(5,5\right)$ $\left(6,4\right)$

$X=11$ のとき： $\left(5,6\right)$ $\left(6,5\right)$

$X=12$ のとき： $\left(6,6\right)$

となる．よって，各確率変数 $X$ の値の確率は

$f\left(2\right)=P\left(X=2\right)={\displaystyle \frac{1}{36}}$ ， $f\left(3\right)=P\left(X=3\right)={\displaystyle \frac{1}{18}}$ ， $f\left(4\right)=P\left(X=4\right)={\displaystyle \frac{1}{12}}$ ， $f\left(5\right)=P\left(X=5\right)={\displaystyle \frac{1}{9}}$ ， $f\left(6\right)=P\left(X=6\right)={\displaystyle \frac{5}{36}}$ ， $f\left(7\right)=P\left(X=7\right)={\displaystyle \frac{1}{6}}$ ， $f\left(8\right)=P\left(X=8\right)={\displaystyle \frac{5}{36}}$ ， $f\left(9\right)=P\left(X=9\right)={\displaystyle \frac{1}{9}}$ ， $f\left(10\right)=P\left(X=10\right)={\displaystyle \frac{1}{12}}$ ， $f\left(11\right)=P\left(X=11\right)={\displaystyle \frac{1}{18}}$ ， $f\left(12\right)=P\left(X=12\right)={\displaystyle \frac{1}{36}}$

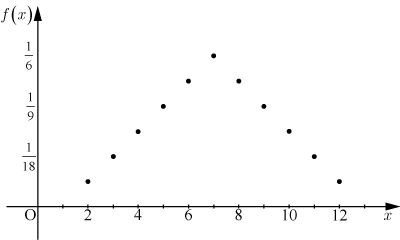
となる．確率関数のグラフは以下の図のようになる.

　

ホーム>>カテゴリー分類>>確率統計>>確率関数>>離散型確率分布

最終更新日： 2025年4月27日

[ページトップ]

利用規約

google translate (English version)