2次不等式の解

●判別式 ${\displaystyle D=b^2-4ac>0}$ のとき

◆ $a{x}^2+bx+c>0$ の解は

実数全体

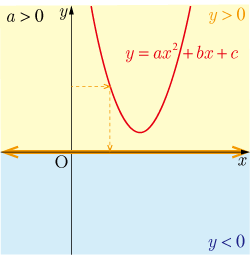
◆ ${\displaystyle a{x}^2+bx+c<0}$ の解は

解なし

●判別式 ${\displaystyle D=b^2-4ac=0}$ のとき

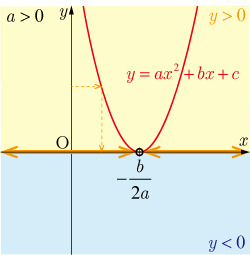
${\displaystyle f\left(x\right)=0}$ は重解を持ち，その解は${\displaystyle x=-\frac{b}{2a}}$ である．よって

◆ $a{x}^2+bx+c>0$ の解は

${\displaystyle x=-\frac{b}{2a}}$ を除く実数全体

◆ ${\displaystyle a{x}^2+bx+c<0}$ の解は

解なし．

●判別式 ${\displaystyle D=b^2-4ac>0}$ のとき

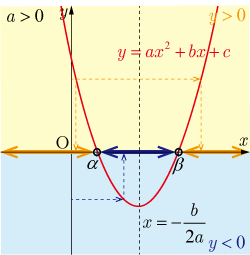
${\displaystyle f\left(x\right)=0}$ は2つの異なる実数解を持つ.その解を${\displaystyle \alpha }$ ， ${\displaystyle \beta }$ ，ただし， ${\displaystyle \alpha <\beta }$ とする．

${\displaystyle \alpha =\frac{-b-\sqrt{b^2-4ac}}{2a}}$， ${\displaystyle \beta =\frac{-b+\sqrt{b^2-4ac}}{2a}}$

◆ $a{x}^2+bx+c>0$ の解は

${\displaystyle x<\alpha }$ ， ${\displaystyle x>\beta }$

◆ ${\displaystyle a{x}^2+bx+c<0}$ の解は

${\displaystyle x<\alpha }$ ， ${\displaystyle x>\beta }$

$•$ 導出

【 $a{x}^2+bx+c>0$ の場合】

$a{x}^2+bx+c>0$ は以下のように書き直すことができる．

${\displaystyle a\left(x-\alpha \right)\left(x-\beta \right)>0}$　･･････(4)

両辺を $a$ で割る ${\displaystyle a>0}$ より符号の向きは変わらない．不等号の性質を参照．

${\displaystyle \left(x-\alpha \right)\left(x-\beta \right)>0}$　･･････(5)

(5)が成り立つのは

${\displaystyle x-\alpha >0}$ かつ ${\displaystyle x-\beta >0}$　･･････(6)

あるいは

${\displaystyle x-\alpha <0}$ かつ ${\displaystyle x-\beta <0}$　･･････(7)

の場合である．

(6)の場合

${\displaystyle x>\alpha }$ かつ${\displaystyle x>\beta }$

${\displaystyle \alpha <\beta }$ より

${\displaystyle x>\beta }$　･･････(8)

となる．

(7)の場合

${\displaystyle x<\alpha }$ かつ${\displaystyle x<\beta }$

${\displaystyle \alpha <\beta }$より

${\displaystyle x<\alpha }$　･･････(9)

となる．

(8)，(9)より(4)の解は

${\displaystyle x<\alpha }$ ， ${\displaystyle x>\beta }$

となる．

【 $a{x}^2+bx+c<0$ の場合】

${\displaystyle a{x}^2+bx+c<0}$ は以下のように書き直すことができる．

${\displaystyle a\left(x-\alpha \right)\left(x-\beta \right)<0}$　･･････(10)

両辺を $a$ で割る ${\displaystyle a>0}$ より符号の向きは変わらない．不等号の性質を参照．

${\displaystyle \left(x-\alpha \right)\left(x-\beta \right)<0}$　･･････(11)

(5)が成り立つのは

${\displaystyle x-\alpha >0}$ かつ ${\displaystyle x-\beta <0}$　･･････(12)

あるいは

${\displaystyle x-\alpha <0}$ かつ ${\displaystyle x-\beta >0}$　･･････(13)

の場合である．

(12)の場合

${\displaystyle x>\alpha }$ かつ${\displaystyle x<\beta }$

${\displaystyle \alpha <\beta }$ より

${\displaystyle \alpha <x<\beta }$ 　･･････(14)

となる．

(13)の場合

${\displaystyle x<\alpha }$ かつ${\displaystyle x>\beta }$

${\displaystyle \alpha <\beta }$より

解なし　･･････(15)

となる．

(14)，(15)より(4)の解は

${\displaystyle \alpha <x<\beta }$

となる．

■ ${\displaystyle a<0}$ （${\displaystyle f\left(x\right)}$ が上に凸のグラフ）の場合

(1)，(2)の両辺に ${\displaystyle -1}$ を掛けると， $x^2$ の係数が正になる，以降は， ${\displaystyle a>0}$ の場合同様にして解く．