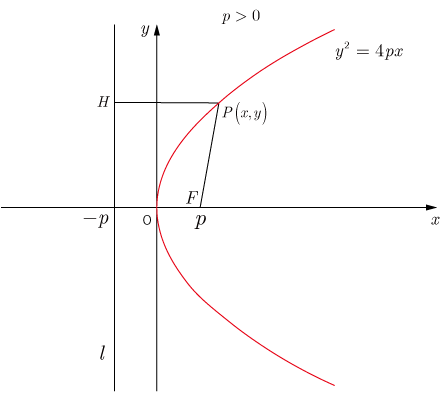■解法のヒント

■new YouTube動画

■三角関数

■ベクトル

■指数/対数

■微分方程式

■級数展開

■線形代数

■ラプラス変換

■チャットボット

関連するページを見るにはこのグラフ図を利用してください．

応用分野： 2次関数のグラフ　y=x^2 ， 2次関数のグラフ　y=a(x^2-p)+q ，離心率， 2次曲線， 2次曲線の分類，円錐曲線，退化円錐， 2次曲線の標準化， 2次曲線の標準化の定理2の証明， 2次曲線：無心の場合の標準化の例

問題リスト←このページに関連している問題です

放物線 (parabola)

■ 放物線の定義

parabola

下図の点Pを動かして定義を確かめてみよう

JSXGraph Copyright (C) see http://jsxgraph.org

平面において， $F$ 点と，この点を通らない直線 $l$ からの距離が等しい点の軌跡が放物線である．

このとき， $F$ を焦点， $l$ を準線という．

■ 放物線の方程式

● 焦点が $x$ 軸上の場合

焦点の座標 $(p, 0)$ ，準線 $x = - p$ の放物線の方程式は

$y^{2} = 4 p x$ $(p \neq 0)$

と表せる．これを標準形という．

頂点 $(0, 0)$ ，焦点 $(p, 0)$ ，準線 $x = - p$

● 焦点が $y$ 軸上の場合

焦点の座標 $(0, p)$ ，準線 $y = - p$ の放物線の方程式は

$x^{2} = 4 p y$ $(p \neq 0)$

と表せる．これを標準形という．

頂点 $(0, 0)$ ，焦点 $(0, p)$ ，準線 $y = - p$

2次関数のグラフ $y = x^{2}$ のページも参考にするとよい．

ホーム>>カテゴリー別分類>>関数>>2次関数

最終更新日： 2024年9月18日

[ページトップ]

$金沢工業大学$

google translate (English version)