外分点

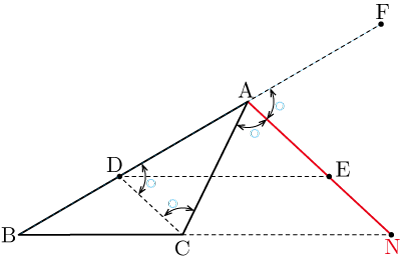
三角形のある頂点の外角の二等分線とその頂点の対辺の延長線との交点を，その対辺の外分点という．

具体例を上げて説明する．三角形 $\text{ABC}$ の頂点 $\text{A}$ の外角の二等分線と辺 $\text{BC}$ の延長線との交点を $\text{N}$ とする．この交点 $\text{N}$ が辺 $\text{BC}$ の外分点である．そして

$\text{AB}:\text{AC}=\text{BN}:\text{CN}$

の関係がある．

• 線分をｍ：ｎに外分する点の位置ベクトル
• 線分の外分点(複素平面)

■証明

線分 $\text{AN}$ と平行で点 $\text{C}$ を通る直線と辺 $\text{AB}$ との交点を点 $\text{D}$ とする．点 $\text{D}$ を通り辺 $\text{BC}$ に平行な直線と線分 $\text{AN}$ との交点を点 $\text{E}$ とする．辺 $\text{AB}$ の延長線上に図のように点 $\text{F}$ をとる．

頂点 $\text{A}$ の外角の二等分線が線分 $\text{AN}$ より

$\angle \text{NAF}=\angle \text{NAC}$ ･･････(1)

$\text{AN}$ // $\text{DC}$ ，かつ， $\angle \text{ADC}$ と $\angle \text{FAN}$ が同位角の関係より

${\displaystyle \angle \text{ADC}=\angle \text{FAN}}$ ･･････(2)

$\text{AN}$ // $\text{DC}$ ，かつ， $\angle \text{ACD}$ と $\angle \text{CAN}$ が錯角の関係より

${\displaystyle \angle \text{ACD}=\angle \text{CAN}}$ ･･････(3)

となる．(1)，(2)，(3)より

${\displaystyle \angle \text{ADC}=\angle \text{ACD}}$ ･･････(4)

(4)より $△\text{ADC}$ は二等辺三角形である．よって

${\displaystyle \text{AD}=\text{AC}}$ ･･････(5)

$\text{DE}$ // $\text{CN}$ ， $\text{DC}$ // $\text{EN}$ より四角形 $\text{DCNE}$ は平行四辺形である．よって

${\displaystyle \text{DE}=\text{CN}}$ ･･････(6)

である．

$△\text{ABN}$ と $△\text{ADE}$ に関して

$\text{BN}$ // $\text{DE}$ ，かつ， $\angle \text{ABN}$ と $\angle \text{ADE}$ が同位角より

$\angle \text{ABN}=\angle \text{ADE}$ ･･････(7)

また

$\angle \text{BAN}=\angle \text{DAE}$   （∵同じ角）　･･････(8)

である．

(7)，(8)より，二つの角が等しい．よって

$△\text{ABN}$ ∽ $△\text{ADE}$

である．したがって

$\text{AB}:\text{AD}=\text{BN}:\text{DE}$ ･･････(9)

である．

(9)に(5)，(6)を代入すると

$\text{AB}:\text{AC}=\text{BN}:\text{CN}$

が得られる．

 

ホーム>>カテゴリー分類>>幾何>>外分点

最終更新日 ： 2025年11月25日

[ページトップ]

利用規約

google translate (English version)