外心の求め方

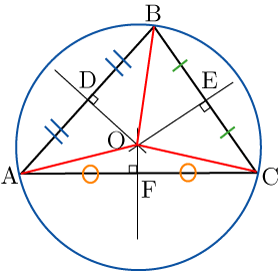
三角形ABCの外心O

A $(x_{1}, y_{1})$ , B $(x_{2}, y_{2})$ , C $(x_{3}, y_{3})$ を頂点とする三角形の外心の求め方

三角形ABCの外接円の半径を $r$ とし，外心の座標を $(p, q)$ とすると，三角形の各々の頂点は半径 $r$ ，中心 $(p, q)$ の円周上にあるので，以下の3つの式を満たす．

${(x_{1} - p)}^{2} + {(y_{1} - q)}^{2} = r^{2}$   ･･････(1)
${(x_{2} - p)}^{2} + {(y_{2} - q)}^{2} = r^{2}$   ･･････(2)
${(x_{3} - p)}^{2} + {(y_{3} - q)}^{2} = r^{2}$   ･･････(3)

式(1)－式(2) より

$x_{1}^{2} - x_{2}^{2} - 2 (x_{1} - x_{2}) p + y_{1}^{2} - y_{2}^{2}$ $- 2 (y_{1} - y_{2}) q = 0$ ･･････(4)

式(2)－式(3) より

$x_{2}^{2} - x_{3}^{2} - 2 (x_{2} - x_{3}) p + y_{2}^{2} - y_{3}^{2}$ $- 2 (y_{2} - y_{3}) q = 0$ ･･････(5)

が得られるので，式(4) $\times (y_{2} - y_{3})$ －式(5) $\times (y_{1} - y_{2})$ より，外心の $x$ 座標

$p = \frac{1}{2} \cdot \frac{(x_{1}^{2} + y_{1}^{2}) (y_{2} - y_{3}) + (x_{2}^{2} + y_{2}^{2}) (y_{3} - y_{1}) + (x_{3}^{2} + y_{3}^{2}) (y_{1} - y_{2})}{(x_{1} - x_{2}) (y_{2} - y_{3}) - (x_{2} - x_{3}) (y_{1} - y_{2})}$

が求まり，式(4) $\times (x_{2} - x_{3})$ －式(5) $\times (x_{1} - x_{2})$ より，外心の $y$ 座標

$q = \frac{1}{2} \cdot \frac{(x_{1}^{2} + y_{1}^{2}) (x_{2} - x_{3}) + (x_{2}^{2} + y_{2}^{2}) (x_{3} - x_{1}) + (x_{3}^{2} + y_{3}^{2}) (x_{1} - x_{2})}{(x_{2} - x_{3}) (y_{1} - y_{2}) - (x_{1} - x_{2}) (y_{2} - y_{3})}$

が求まる．

ホーム>>カテゴリー分類>>幾何>>外心>>外心の求め方

最終更新日：2023年6月21日