三角形の頂点の二等分線の性質
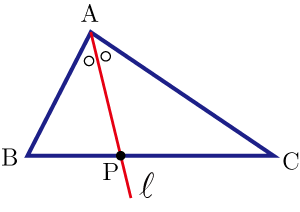
頂点の角の二等分線を とし,との交点を(内分点)とすると
である.
■証明
頂点
,頂点Cから二等分線に垂線を下ろし,それぞれの垂線の足を
,
とする.
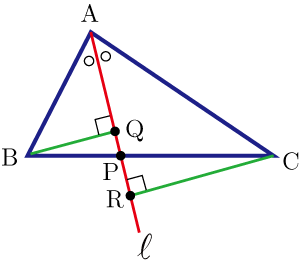
△
と△
について考える.
(∵
は∠の二等分線)
(∵,は垂線の足であるから)
より,2角が等しいので
△∽△
よって
・・・・・・(1)
次に,△と△を考える.
(∵対角)
(∵,は垂線の足であるか)
より,2角が等しいので
△∽△
よって
・・・・・・(2)
(1),(2)より
ホーム>>カテゴリー分類>>幾何>>三角形の頂点の二等分線の性質
最終更新日
:
2023年10月2日