|
|||||||||||||
|
|||||||||||||
|
三角錐の体積
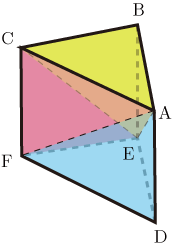 三角錐の体積=底面積×高さ×
三角錐の体積=底面積×高さ×
■証明
三角柱を3つの三角錐に分解することで証明する.
(Ⅰ)三角錐 と三角錐 について三角柱 の側面の四角形 は平行四辺形である.
よって
・・・・・・(1)
・・・・・・(2)
となる.
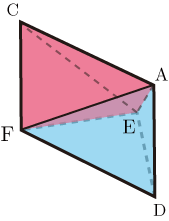 次に,
と
について考える.
次に,
と
について考える.
(1),(2)とが共通であることより
が成り立ち
の面積= の面積 ・・・・・(3)
となる.
□ を底面とする四角錐はで三角錐と三角錐 に2分割される.(3)より底面が面積の等しい三角形に分割されているので
三角錐 の体積=三角錐 の体積 ・・・・・・(4)
が成り立つ.
(Ⅱ)三角錐 と三角錐 について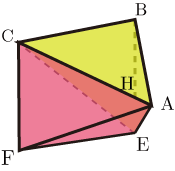
三角柱 の側面□ は平行四辺形である.
よって
・・・・・・(5)
・・・・・・(6)
となる.
次に, と について考える.
(5),(6)と が共通であることより
が成り立ち
の面積= の面積 ・・・・・(7)
となる.
□ を底面とする四角錐 は で三角錐 と三角錐 に2分割される.(6)より底面が面積の等しい三角形に分割されているので
三角錐 の体積=三角錐 の体積 ・・・・・・(8)
が成り立つ.
(4),(8)より
三角錐の体積=三角錐 の体積(三角錐の体積)=三角錐 の体積 ・・・・・・(9)
となり3つの三角錐の体積は等しい.
よって,
を底面とする三角錐(三角錐)の体積=×三角柱 の体積 ・・・・・・(10)
となる.
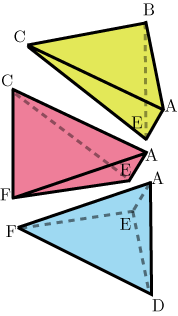
また
を底面とする三角錐 (三角錐 )の高さは,三角柱 の高さと等しい ・・・・・・(11)
(10),(11)より三角錐の体積は,
三角錐の体積=底面積×高さ×
となる.
最終更新日: 2024年1月29日