|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこの知識グラフを利用してください.
直線 に関して対称
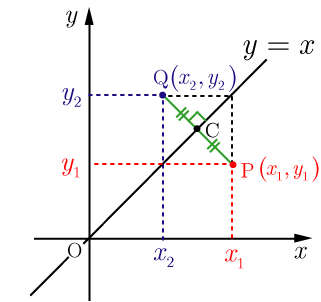 2点
,
が直線
に関して対称であることは
2点
,
が直線
に関して対称であることは
が成り立つことと同値である.
すなわち,点 の 直線 に関して対称な点 の座標は となり 成分と 成分が入れ替わっている.
■証明
点 の 成分と 成分入れ替えた点を とする.
線分 の傾きを とすると
直線 の傾き は1であるから
(2直線が垂直に交わる条件を参照)
となり
直線 は直線 に垂直 ・・・・・・(1)
である.点 , の中点を とすると
,
となり
・・・・・・(2)
である.
よって,(1),(2)より定直線に関して対称な点であるための条件を満たしているので点 ,点 は直線 に関して対称である.
ホーム>>カテゴリー別分類>>幾何>>定直線に関して対称(線対称)>> に関して対称な点
最終更新日 2025年1月17日