|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこの知識グラフを利用してください.
補数による減算
■負の数の表現
コンピュータでは,負の数を扱えない.そこで補数によって負の数を表現する.
ある正の2進数 に対して
( の補数)
と定義する.
10進数で から7に対応する2進数の値を4桁で下表に示す.
すなわち,4桁まで扱えるコンピュータを考える.
10進数で1から7までの正の値の2進数の4桁目は0になっている.
そのため,2の補数では4桁目が1となる.
つまり,負の数は最上位桁が1となっていることがわかる.
■補数による計算
2の補数を,負の数と表現することで加算を足し算で行える.
例えばある正の2進数 があるとする.
の 補数 →補数の定義
の 補数 ・・・・・・(1)
補数の定義より, を補数で表せる.
(∵(1))
=
なので,減算を2の補数で行える.
また, は(桁数+1)を桁打ち消すものである.
あふれた桁を無視すれば同じ処理となる.
-
普通の計算
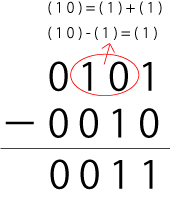
-
補数を使った計算

最終更新日:
2025年4月25日