|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこのグラフ図を利用してください．
応用分野：
16進数から2進数へ変換，
補数の定義
■補数とは
コンピュータ内での四則演算は，全て加算処理で計算される．
補数を使えば減算を加算で行うことができる．
補数とは， n 進数の数に加算すると1桁上がる数の最小値，もしくは桁上がりしない最大値となる数のことである．
n 進数では前者を n の補数，後者を n−1 の補数という．
例えば，2進数8桁10011010についての補数は
1の補数(01100101)2
2の補数(01100110)2
である．
■1の補数について
1の補数は，2進法である数 n に加算すると桁上がりしない最大値となる数のことである．
n + ( n の1の補数 ) =(111⋅⋅⋅⋅1)2 ← ( n の桁数 ) 桁
( n の1の補数 ) =(111⋅⋅⋅⋅1)2−n
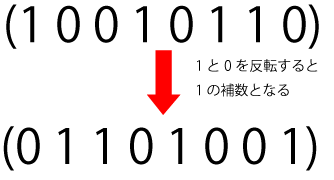
式より，全て1である n と同じ桁数の数から n を引くと( n の1の補数)が求まる．
また実際に上記の計算をすると，( n の1の補数)はnの1と0を反転したものであることがわかる．
■2の補数について
2の補数は，2進法である数 nに加算するとnの桁数+1 の桁で，最小値となる数のことである．
n + ( n の2の補数 ) =(100⋅⋅⋅⋅0)2 ← ( n の桁数 + 1 ) 桁
( n の2の補数 ) =(100⋅⋅⋅⋅0)2−n
( n の2の補数 ) =(111⋅⋅⋅⋅1)2−n+(1)2
式より， n の桁数 +1 の桁の最小値100⋅⋅⋅⋅0 からn を引くと( n の2の補数 )が求まる．
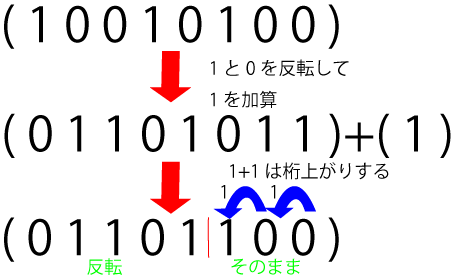
また2の補数は n の1と0を反転して1を加算したもの， つまり n の1である最小桁以下を反転せず，それ以上の桁を反転したものである．
最終更新日： 2023年10月7日
