三角比の定義

■ 角度 $θ$ $θ$ が $0 ° ≦ θ < 90 °$ $0 ° ≦ θ < 90 °$ の場合

●正弦（sine）の定義

$sin θ = \frac{BC}{AB}$ $sin θ = \frac{BC}{AB}$

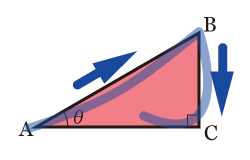
sinのsの筆記体の筆順の順に分母，分子となる．

●余弦（cosine）の定義

$cos θ = \frac{AC}{AB}$ $cos θ = \frac{AC}{AB}$

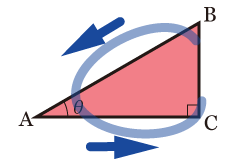
cosのcの筆記体の筆順の順に分母，分子となる､．

●正接（tangent）の定義

$tan θ = \frac{BC}{AC}$ $tan θ = \frac{BC}{AC}$

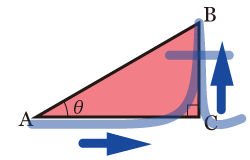
tanのtの筆記体の筆順の順に分母，分子となる．

■角度 $θ$ $θ$ が任意の場合

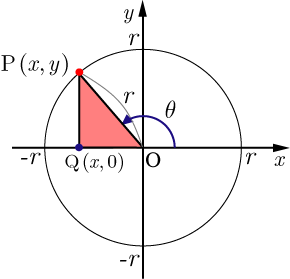角度 $θ$ $θ$ が任意の場合の三角比について説明する． $x y$ $x y$ 座標平面状上に原点Oを中心として，半径 $r$ $r$ の円を描く．その円周上に点Pをとる．OPと $x$ $x$ 軸とのなす角度が $θ$ $θ$ となる．点Pから $x$ $x$ 軸に垂線を下ろしその交点をQとした△OPQを考える．点Pの座標を $(x, y)$ $(x, y)$ ，点Qの座標を $(x, 0)$ $(x, 0)$ とする．参考ページ：x軸の正方と線分OPのなす角

● $sin θ = \frac{y}{r}$ $sin θ = \frac{y}{r}$

( $| sin θ | = \frac{PQ}{OP}$ $| sin θ | = \frac{PQ}{OP}$ 符号：点Pが第1，第2象限は正，第3，第4象限は負 )

● $cos θ = \frac{x}{r}$ $cos θ = \frac{x}{r}$

( $| cos θ | = \frac{OQ}{OP}$ $| cos θ | = \frac{OQ}{OP}$ 符号：点Pが第1，第4象限は正，第2，第3象限は負 )

● $tan θ = \frac{y}{x}$ $tan θ = \frac{y}{x}$

( $| tan θ | = \frac{PQ}{OQ}$ $| tan θ | = \frac{PQ}{OQ}$ 符号：点Pが第1，第3象限は正，第2，第4象限は負 )

ただし，

$r = \sqrt{x^{2} + y^{2}}$ $r = \sqrt{x^{2} + y^{2}}$

特に，半径が1の場合の右図の円のことを単位円といい，

$sin θ = y$ $sin θ = y$ ， $cos θ = x$ $cos θ = x$

となり，点Pの $y$ $y$ 座標が正接（sine）， $x$ $x$ 座標が余弦(cosine)となる．

ホーム>>カテゴリー分類>>三角関数>>三角比の定義

最終更新日： 2025年2月13日

三角比の定義

●正弦（sine）の定義

●余弦（cosine）の定義

●正接（tangent）の定義

■角度 θθ<math xmlns="http://www.w3.org/1998/Math/MathML"> <mi>θ</mi> </math> が任意の場合

● sinθ=yrsinθ=yr<math xmlns="http://www.w3.org/1998/Math/MathML"> <mstyle displaystyle="true"> <mo>sin</mo> <mi>θ</mi> <mo>=</mo> <mfrac> <mi>y</mi> <mi>r</mi> </mfrac> </mstyle> </math>

● cosθ=xrcosθ=xr<math xmlns="http://www.w3.org/1998/Math/MathML"> <mstyle displaystyle="true"> <mo>cos</mo> <mi>θ</mi> <mo>=</mo> <mfrac> <mi>x</mi> <mi>r</mi> </mfrac> </mstyle> </math>

● tanθ=yxtanθ=yx<math xmlns="http://www.w3.org/1998/Math/MathML"> <mstyle displaystyle="true"> <mo>tan</mo> <mi>θ</mi> <mo>=</mo> <mfrac> <mi>y</mi> <mi>x</mi> </mfrac> </mstyle> </math>

Chat window

■角度 $θ$ $θ$ が任意の場合

● $sin θ = \frac{y}{r}$ $sin θ = \frac{y}{r}$

● $cos θ = \frac{x}{r}$ $cos θ = \frac{x}{r}$

● $tan θ = \frac{y}{x}$ $tan θ = \frac{y}{x}$