組み立て除法

整式の割り算(除法) $(a x^{3} + b x^{2} + c x + d) \div (x - p)$ の商を $l x^{2} + m x + n$ ，余りを $q$ とする（割る数は $x$ の1次式で $x$ の係数は1とする）．式で表すと，

$a x^{3} + b x^{2} + c x + d$ $= (l x^{2} + m x + n) (x - p) + q$

となる．

上式の右辺を展開して整理すると，

$a x^{3} + b x^{2} + c x + d$ $= l x^{3} + (m - p l) x^{2} + (n - p m) x + q - p n$

となる．この等式がすべての $x$ に対して恒に成り立つためには，左辺と右辺の各次数の項の係数の値および定数項の値が等しくなければならない．よって，

${\begin{cases} a = l \\ b = m - p l \\ c = n - p m \\ d = q - p n \end{cases}$

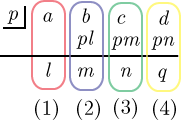組み立て除法の式が成り立つ必要がある．この式を変形し

${\begin{array}{l} l = a & \dots \dots (1) \\ m = b + p l & \dots \dots (2) \\ n = c + p m & \dots \dots (3) \\ q = d + p n & \dots \dots (4) \end{array}$

とし，右上表のような形式で，(1)，(2)，(3)，(4)の式に従って， $l$ ， $p l$ ， $m$ ， $p m$ ， $n$ ， $p n$ ， $q$ の値を記述する．この様な表を作成して商と余りを求める方法を組み立て除法という．

■具体的な計算例

$(2 x^{3} - 7 x^{2} + 7 x + 3) \div (x - 2)$ の商と余りを組み立て除法で求める．⇒ここページに記載

■組み立て除法と筆算の比較

$(2 x^{3} - 7 x^{2} + 7 x + 3) \div (x - 2)$ の商と余りの計算の組み立て除法と筆算の比較⇒ここページに記載

ホーム>>カテゴリー別分類>>数と式>>組み立て除法

最終更新日： 2024年5月7日