関連するページを見るにはこのグラフ図を利用してください．

不等式の性質

$A$ ，$B$ ，$C$ ，$D$ は数または式で，${\displaystyle C>0}$，${\displaystyle D=-C<0}$ とする．ただし， $A$ ，$B$ ，$C$ ，$D$ は実数とする．

以下の内容は，「$>$ ， $<$ 」 の代わりに 「$\geqq$ ， $\leqq$ 」の場合でも成り立つ．

${\displaystyle A>B}$ ならば

1. ${\displaystyle A+C>B+C}$　（不等式の両辺に同じ数や式を加えても不等号の向き変わらない）

   

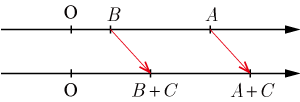
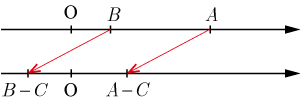
2. ${\displaystyle A-C>B-C}$　（不等式の両辺から同じ数や式を減じても不等号の向きは変わらない）

   

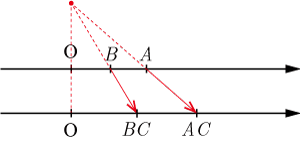
3. ${\displaystyle AC>BC}$　（不等式の両辺に同じ正の数あるいは正の値の式を掛けても不等号の向きは変わらない）

   

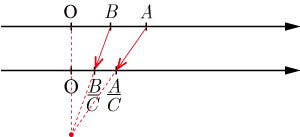
4. ${\displaystyle \frac{A}{C}>\frac{B}{C}}$　（不等式の両辺を同じ正の数あういは正の値の式で割っても不等号の向きは変わらない）

   

5. ${\displaystyle -A<-B}$　（不等式の両辺に ${\displaystyle -1}$ を掛けると不等号の向きが変わる）

   

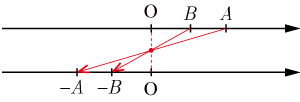
6. ${\displaystyle AD<BD}$ 　（不等式の両辺に負の数あるいは負の値の式を掛けると不等号の向きが変わる）

   【考え方】

   まず，両辺に $C$ を掛ける.

   ${\displaystyle AC>BC}$

   次に，両辺に ${\displaystyle -1}$ を掛ける. 不等号の向きが変わることに注意

   ${\displaystyle -AC<-BC}$

   ${\displaystyle -C=D}$ より，式を書きかえる．

   ${\displaystyle AD<BD}$

7. ${\displaystyle \frac{A}{D}<\frac{B}{D}}$ 　（不等式の両辺を負の数あるいは負の値の式で割ると不等号の向きが変わる）

   【考え方】

   まず，両辺を $C$ で割る.

   ${\displaystyle \frac{A}{C}>\frac{B}{C}}$

   次に，両辺に ${\displaystyle -1}$ を掛ける. 不等号の向きが変わることに注意

   ${\displaystyle -\frac{A}{C}<-\frac{B}{C}}$

   ${\displaystyle -C=D}$ より，式を書きかえる．

   ${\displaystyle \frac{A}{D}<\frac{B}{D}}$

 

ホーム>>カテゴリー別分類>>数と式>>不等式の性質

最終更新日： 2024年9月25日

[ページトップ]

利用規約

google translate (English version)