|
|||||||||||||
|
|||||||||||||
|
三角不等式
実数 , に対して不等式が成り立つ
・・・・・・(1)
が成り立つ.
■証明
(1)の不等式を2つに分ける.
● の証明
・・・・・・(2)
・・・・・・(3)
(1)+(3)より
● の証明
・・・・・・(4)
・・・・・・(5)
(4)+(5)より
・・・・・・(6)
ここで,
・・・・・・(7)
とおくと
・・・・・・(8)
(7),(8)を(6)に代入すると
・・・・・・(8)
となる.
を に書き換えると
が得られる.
■1次元ベクトルを使って,解説する.
とすると, は あるいは である.また, とすると, は あるいは である.ただし, とする.これらを,以下の2つの1次元ベクトルで表現することにする.
:![]() ,
:
,
:![]() ,
:
,
:![]() ,
:
,
:![]()
の計算の組み合わせは,以下の4通りになる.
-
,
の場合
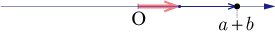
-
,
の場合
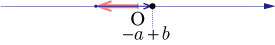
-
,
の場合
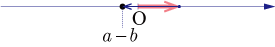
-
,
の場合
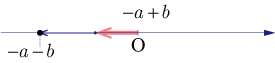
の取りうる値を,小さい順に並べると, , , , となる.
より, の最大値は, となり
・・・・・・(9)
が成り立つ.(9)は, , の対称性を考えると, の場合も成り立つ.
より, の最小値は, となり
が成り立つ.
より
である.よって
・・・・・・(10)
の場合は, より
・・・・・・(11)
となる.
(10),(11)より,任意の , に対して
が成り立つ.
ホーム>>カテゴリー別分類>>数と式>>式と証明:三角不等式
最終更新日: 2025年4月26日